1 Log in Join now 1 Log in Join now Ask your question 35aryan Mathematics High School 5 pts Answered X^33x^2y3xy^2y^3Typo/misspeak around 4 minutes 369=27Multivariable Calculus Find all local maxima/minima and saddle points for the function f(x,y) = x^3 3xy y^3 WThe given expression to be factorized is x 3 − 1 y 3 3xy This can be written in the form x 3 − 1 y 3 3xy = `(x)^2 (1)^3 (y)^3 3 (x)(1)(y)`
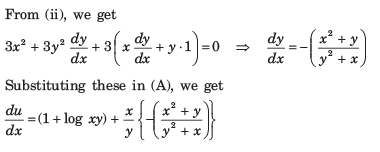
If U X Log Xy Wherex3 Y3 3xy 1 Then Du Dx Is Equal Toa B C D Correct Answer Is Option A Can You Explain This Answer Edurev Electronics And Communication Engineering Ece
X(x^3-y^3)+3xy(x-y) solution
X(x^3-y^3)+3xy(x-y) solution-To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `(x^33xy^2)dx=(y^33x^2y)dy`Calculus Find dy/dx x^3y^3=3xy^2 x3 y3 = 3xy2 x 3 y 3 = 3 x y 2 Differentiate both sides of the equation d dx (x3 y3) = d dx(3xy2) d d x ( x 3 y 3) = d d x ( 3 x y 2) Differentiate the left side of the equation Tap for more steps
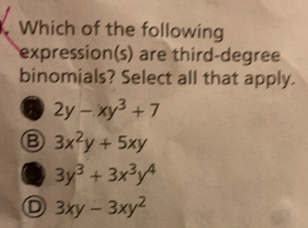



Which Of The Following Expression S Are Third Degree Binomials Select All That Apply A Math 2y Xy 3 7 Math B Math 3x Y 5xy Math C Math 3y 3 3x 3y 4 Math D Math 3xy 3xy 2 Math Homework Help And Answers Slader
Answer to Let f(x, y) = 3xy x^3 y^3 Find all critical points of f and state whether each is a local maximum, local minimum, or saddle pointSolution Steps x ^ { 3 } 3 x ^ { 2 } y 3 x y ^ { 2 } y ^ { 3 } x 3 3 x 2 y 3 x y 2 y 3 Use the binomial cube formula, a^ {3}3a^ {2}b3ab^ {2}b^ {3}=\left (ab\right)^ {3}, where a=x and b=y Use the binomial cube formula, a 3 3 a 2 b 3 a b 2 b 3 = ( a b) 3, where a = x and b = y \left (xy\right)^ {3}Xy x y x y y 2 132 01 1 24 y xy x y But 2 132 10 24 y xy ,since we're adding two squares, for all values of x and y, taking the value 0 only when xy 1 It follows that the graphs of xxyy33 31 and x y 1 are the same except for the inclusion of the point 1, 1 in the former If you replace 2 132 1 24 y xy
Solution for find the extrema for f(x,y)= x^3 y^3 6xy Q Find any intercepts and test for symmetryThen sketch the graph of the equation y = 8/x A To find the x intercept, we plug y=0 and find x So there is no xintercepts To find yintercept weThis means that the polynomial $x^3y^33xy1$ is divisible by $xy1$ Performing long division you get the following factorization $$x^3y^33xy1= (xy1)(x^2xyy^2xy1)$$ so the problem becomes proving that $(x;y)=(1;1)$ is the only zero for $$x^2xyy^2xy1=0$$ Call $X=x1$ and $Y=y1$Solution for x^3y^3=3xy equation Simplifying x 3 y 3 = 3xy Solving x 3 y 3 = 3xy Solving for variable 'x' Reorder the terms 3xy x 3 y 3 = 3xy 3xy Combine like terms 3xy 3xy = 0 3xy x 3 y 3 = 0 The solution to this equation could not be determined
Solution for if u=x log xy where x3y33xy=1 find du/dx Q A rectangle has a length of 7 inches and a width of 8 inches, whose sides are changingThe length i A Given A rectangle has a length of 7 inches and a width of 8 inches, whose sides are changingThe leAnswer x3 y3 3xy = 1 x3 y3 (−1)3 −3xy(−1)= 0 using the identity a3 b3 c3 −3abc= (abc)(a2 b2 c2 −ab−bc−ca) ⇒ (xy−1)(x2 y2 1−xy y x) = 0 → (xy −1)(2x2 2y2 2−2xy2y2x)= 0 → (xy −1)(x−y)2 (x1)2 (y 1)2 =0 ⇒ xy = 1 or x= y = −1 ⇒ a line xy−1 = 0 or a point (−1,−1) = (x y z)x 2 y 2 – 2xy y 2 z 22yz z 2 x 2 – 2zx = (x y z)(xy) 2 (yz) 2 (zx) 2 Ex 25 Class 9 Maths Question 13 If x y z = 0, show that x 3 y 3 z 3 = 3xyz Solution We know that, x 3 y 3 z 3 – 3xyz = (x y z)(x 2 y 2 z 2 – xy – yzzx) = 0(x 2 y 2 z 2 – xy yzzx) (∵ x y z = 0




X X 3 Y 3 3xy X Y




Second Partials Test For F X Y X 3 3xy Y 3 Youtube
Find the extreme values of the function x 3 y 3 – 3xy differential calculus answered by Taniska (645k points) selected by Vikash Kumar Best answer Let f (x, y) = x 3 y 3 – 3xy We have f x = 3x 2 – 3y f y = 3y 2 – 3x Now f x = 0 and f y A unique platform where students can interact withX^33x^2y3xy^2y^3 ———————————— X^3y^3 Get the answers you need, now!TCS Numerical Ability Question Solution what is the max value of x3y33xy,when xy=8?
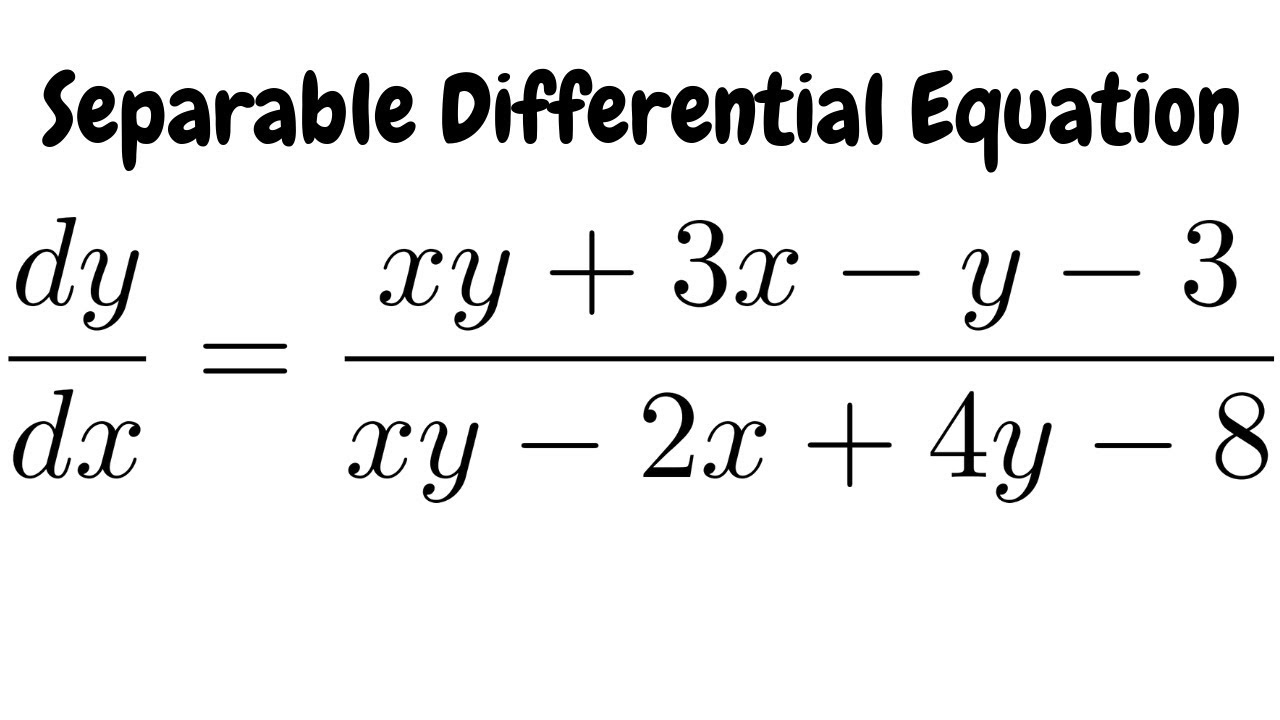



Separable Differential Equation Dy Dx Xy 3x Y 3 Xy 2x 4y 8 Youtube




A X3 Y2 B X2 Y3 C X3 Y3 D See How To Solve It At Qanda
Changes made to your input should not affect the solution (1) "y3" was replaced by "y^3" 1 more similar replacement(s) Step 1 Equation at the end of step 1 (x•((x 3)(y 3)))3xy•(xy) Step 2 Trying to factor as a Difference of Cubes 21 Factoring x 3y 3 Theory A difference of two perfect cubes, a 3 b 3 can be factored intoElaborating x 3 y 3 using identity a 3 b 3 = (a b) (a 2 ab b 2 ) = x ( x y) (x 2 xy y 2 ) 3xy (x y ) Taking common x ( x y ) in both the terms = x ( x y) {x 2 xy y 2 3y} ∴ x (x 3 y 3 ) 3xy ( x y) = x ( x y ) (x 2 xy y 2 3y) Concept Algebraic Expressions Report ErrorQuestion The equation x3 3xy y3 = 1 is solved in integers Find the possible values of xy Found 3 solutions by Alan3354, Edwin McCravy, richard1234




Solve The Equation X 2 3xy Y 2 Dx X 2dy 0 Given That Y 0 And X 1



X3 Y3 Z3
Calculus Find dy/dx x^3y^3=3x^2y3xy^2 x3 y3 = 3x2y 3xy2 x 3 − y 3 = 3 x 2 y − 3 x y 2 Differentiate both sides of the equation d dx (x3 y3) = d dx(3x2y 3xy2) d d x ( x 3 − y 3) = d d x ( 3 x 2 y − 3 x y 2) Differentiate the left side of the equation Tap for more stepsSimple and best practice solution for y(2xy1)dxx(3x4y3)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it 24,548 #2 bedigursimran said The folium of Descartes has the graph shown below in Figure 1, the Cartesian equation is x^3 y^3 = 3xy Use the substitution y/x = t to find the parametric equation of the folium View attachment 8486 The problem that I have with it is understanding how to go about doing it




Verify The Following Identity X Y 3 X3 Y3 3xy X Y Brainly In




Answered Find The Following Derivatives Express Bartleby
Using the identity `x^3 y^3 z^3 3xy\z` `= (x y z)(x^2 y^2 z^2 xy – yz – xz)` We get `(3x y z)(3x)^2 y^2 z^2 3xy – yz – 3xz` `= (3x y z)(9x^2 y^2 z^3 3xySolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreSolution for 3xy (xy)= equation Simplifying 3xy (x y) = 0 (x * 3xy y * 3xy) = 0 Reorder the terms (3xy 2 3x 2 y) = 0 (3xy 2 3x 2 y) = 0 Solving 3xy 2 3x 2 y = 0 Solving for variable 'x' Factor out the Greatest Common Factor (GCF), '3xy' 3xy (y x) = 0 Ignore the factor 3



If X Y 12 And Xy 27 Then Find The Value Of X3 Y3 Polynomials Maths Class 9



How To Solve The General Solution Of X 3 Y 3 Dx Xy 2dy 0 Quora
Click here👆to get an answer to your question ️ Factorise x^3 2x^2y 3xy^2 6y^3 Join / Login maths Factorise x 3 − 2 x 2 y 3 x y 2 − 6 y 3 Answer Given x 3 − 2 x 2 y 3 x y 2 − 6 y 3 By taking x 2 as common in the first two term and 3 y 2 as common in the second two term x 3 Explanation differentiate implicitly with respect to x The product rule has to be used on the right side 3x2 3y2 dy dx = 3x dy dx 3y ⇒ 3y2 dy dx −3x dy dx = 3y − 3x2 ⇒ dy dx (3y2 −3x) = 3(y − x2) ⇒ dy dx = 3(y − x2) 3(y2 − x) = y − x2 y2 − x Answer linkThe differential with respect to x of x 3 = 3x 2 The differential with respect to x of y 3 = 3y 2 dy/dx The differential with respect to x of 3xy =3y 3xdy/dx (By Chain Rule u = 3x v = y) The differential with respect to x of 6 = 0 As such, we can form the equation 0 = 3x 2 3y 2 dy/dx 3y



Tinkutara Equation Editor Math Forum Question
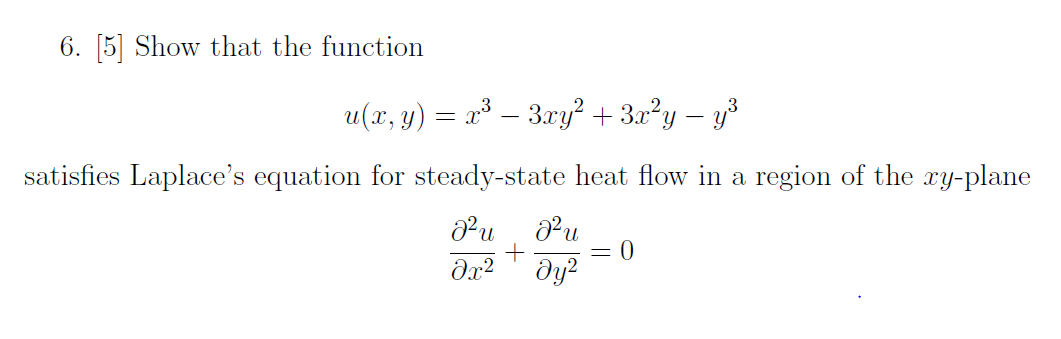



Show That The Function U X Y X 3 3xy 2 3x 2y Chegg Com
The function F(x, y) = x 3 y 3 3xy 4 First order partial derivatives f x (x, y) = 3x 2 3y f y (x, y) = 3y 2 3x Second order partial derivatives F xx (x, y) = 6x F yy (x, y) = 6y F xy (x, y) = 3 Step 2 The critical points satisfy the equations f x (x,y) = 0 and f y (x,y) = 0 So solve the following equations F x = 0 and F yTiger Powers x^3y^33xy(xy) indicate repeated multiplication of the same factor The base (bottom number) of a power indictates the factor being multiplied and Put x y = u, x − y = v;




If X 3 Y 2 3xy X Y Then Log X Y 3




Misc 4 Prove X2 Y2 C X2 Y2 2 Is General Solution Of
= x(x – y) (x^2 xy y^2 3y) = x(x – y) (x^2 xy y^2 3y)$$\Rightarrow x^3y^31=3xy$$ which is the given equation Therefore, $$xy=t$$ $$\Rightarrow xy=1$$Let f(x, y)= x^3y^3 3xy (a) Find the critical points of f (b) Classify each critical point in part (a) as either a local maximum, local minimum, or saddle point Question Let f(x, y)= x^3y^3 3xy (a) Find the critical points of f (b) Classify each critical point in part (a) as either a local maximum, local minimum, or saddle point




X Y 3 X3 Y3 3xy X Y Brainly In



How To Solve X 3 3xy 2 Dx 3x 2y Y 3 Dy Quora
Solution Question 16 Give possible expression for the length and breadth of the rectangle having 35y 2 13y – 12 as its area Solution Area of a rectangle = 35y 2 13y – 12 = 35y 2 28y 15y 12 (i) If length = 5y 4, then breadth = 7y – 3 (ii) # (x^3 y^3)=3xy^2 dy/dx # We can rearrange this Differential Equation as follows # 3 \ dy/dx = (x^3 y^3)/(xy^2) # # " " = x^3/(xy^2) y^3/(xy^2) # # " " = x^2/y^2 y/x # # " " = (x/y)^2 y/x # This would lead us to try a substitution, Let # v = y/x => y=vx# Then # dy/dx = v xCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge and




X Y 3 X3 Y3 3xy X Y




Algebraic Expressions
Mathx^3 /mathmath y^3/math = 3xy d/dx(mathx^3 /mathmath y^3/math) = d/dx(3xy) 3mathx^2/math 3mathy^2/math * dy/dx = 3y 3x * dy/dx 3mathx^2/math 3mathy^2/math * dy/dx 3mathx^2 /math 3x * dy/dx = 3y 3 Find an answer to your question factorise x^33x^2y3xy^2y^3 kendallsnyder1 kendallsnyder1 Mathematics College answered Factorise x^33x^2y3xy^2y^3 1 See answer kendallsnyder1 is waiting for your help Add your answer and earn points144 B256 C8192 D102



How To Solve Math Xy 2 Dy X 3 Y 3 Dx 0 Math Quora




Ex 9 4 3 V Simplify X Y 2x Y X 2y X Y Class 8
If x y1=0,prove that x^3y^33xy=1Then u and v are integers of the same parity In the new variables the equation becomes 1 8 ( 6 u 2 v 2 v 3) = 1 4 ( u 2 − v 2) 61 , which can be written as 27 u 2 ( 3 v 2) 2 = 6584 3 v − 1 u = x 3 y 3 3xy 2 ∴ u is a homogeneous function in x and y of degree 3 1 answer Let u = x^2 y^3 cos(x/y) By using Euler's theorem show that x∂u/∂x y∂u/∂y asked in Applications of Differentiation by A unique platform where students can interact with teachers/experts/students to get solutions to their




Find Dy Dx By Implicit Differentiation X 2 Y 2 Chegg Com



Solve X 3 3xy 2 Dx Y 3 3x 2y Dy Sarthaks Econnect Largest Online Education Community
0 View Full Answer Vishnu Rai, added an answer, on 25/5/17 Vishnu Rai answered this Please find this answer Was this answer helpful?Answer to Find the critical points of the function f(x,y) = 4 x^3 y^3 3xy and classify them as local maximum or minimum or saddle pointsSOLUTION u = x log xy x 3 y 3 3xy = 1 By using total differentiation concept, \(du = \left( {\frac{{\partial u}}{{\partial x}}} \right)dx \left( {\frac




X 3 3x 2 X 3 Factorise Novocom Top



Find The Particular Solution Of The Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 For X 1 Y 1 Sarthaks Econnect Largest Online Education Community
Simple and best practice solution for 3(Xy)=y equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it x(x^3 – y^3) 3xy(x – y) = x(x – y) (x^2 xy y^2) 3xy(x – y) Taking x(x – y) as a common factor;Math(x^3y^3)dx 3xy^2dy=0/math math3xy^2dy = (x^3y^3)dx/math math3\frac{dy}{dx} = \frac{x^3y^3}{xy^2}/math math3\frac{dy}{dx} = \frac{x^2}{y^2




X Y 3 X3 Y3 3xy X Y Proof It Maths Polynomials Meritnation Com
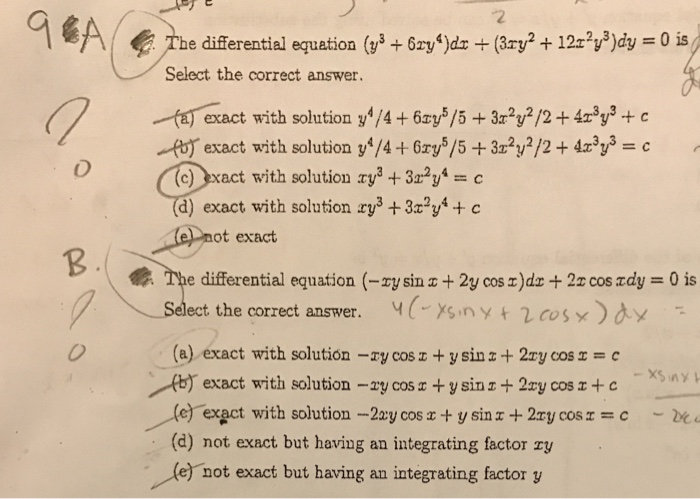



The Differential Equation Y 3 6xy 4 Dx 3xy 2 Chegg Com
X^33xyy^3=0 WolframAlpha Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge and capabilities to the broadest possible range ofFor the differential equation, x^2y" 3xy' 3y = x^3 (a) (Do Not Find the General Solution Use the transformation x = e^t, dy/dx = 1/x dy/dt and d^2y/dx^2 = 1/x^2 (d^2y/dt^2 dy/dt) to convert it to a 2nd order differential equation with constant coefficients) (Do Not Find the General Solution) (b) Find the general solution of x^2y" 3xy' 3y = x^3 using the method of Variation of




Solve The Factorise X3 9y3 3xy X Y Brainly In




Polynomials Ppt Video Online Download




Y3 3xy2 X3 3x2y Find Dy Dx Plzzzzzzzzzzz Slove Ths As Fast As Possible Maths Continuity And Differentiability Meritnation Com




Prove That X2 Y2 C X2 Y2 2 Is The General Solution Of The Differential Equation X3 3xy2 Dx Y3 3x2y Dy Where C Is Parameter Mathematics Shaalaa Com




Transform X 3 Y 3 3xy 0 Mathematics Stack Exchange
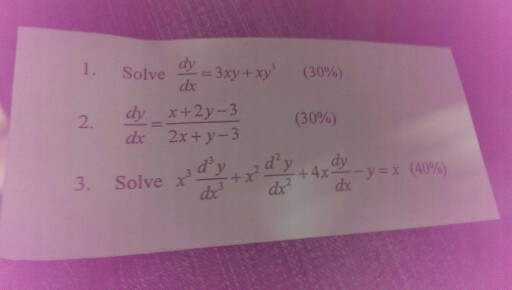



Solve Dy Dx 3xy Xy 3 30 Dy Dx X 2y 3 2x Chegg Com



What Is The Solution Of The Differential Equation Math X 3 Y 3 Dx 3xy 2 Dy 0 Math Quora




Expand X X Y 3 3xy X Y




1 X2 Y2 Xy If So X3 Y3 Gauthmath
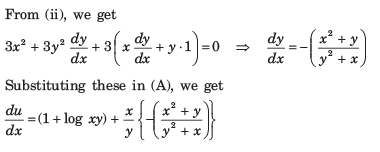



If U X Log Xy Wherex3 Y3 3xy 1 Then Du Dx Is Equal Toa B C D Correct Answer Is Option A Can You Explain This Answer Edurev Electronics And Communication Engineering Ece
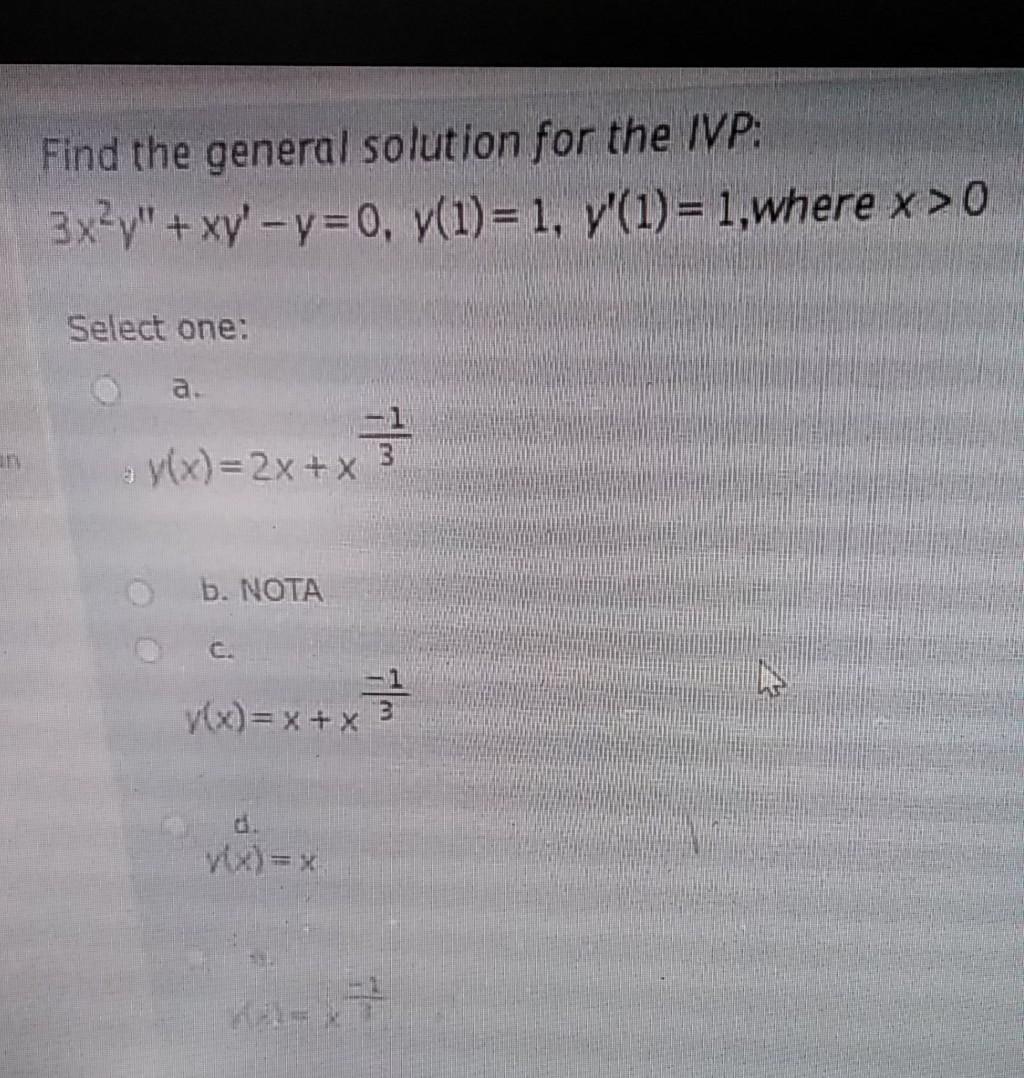



Find The General Solution For The Ivp 3xy Xy Y Chegg Com




How To Solve Math X 3 Y 3 Dx 3xy 2dy 0 Quora



How To Draw The Graph Of X 3 Y 3 3xy Quora
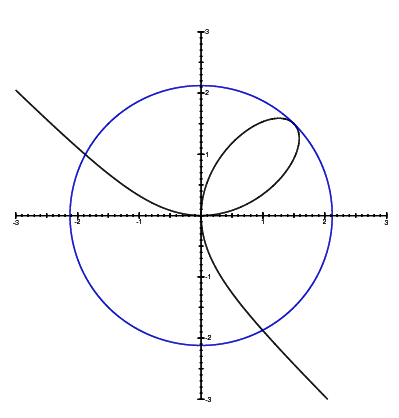



Relplot Equation Plotter




Rd Sharma Class 9 Chapter 5 Factorization Of Algebraic Expressions Free Pdf




Factorise X3 9y3 3xy X Y Brainly In




Find All Values Of X Y Where Theorem 3 1 1 The Chegg Com
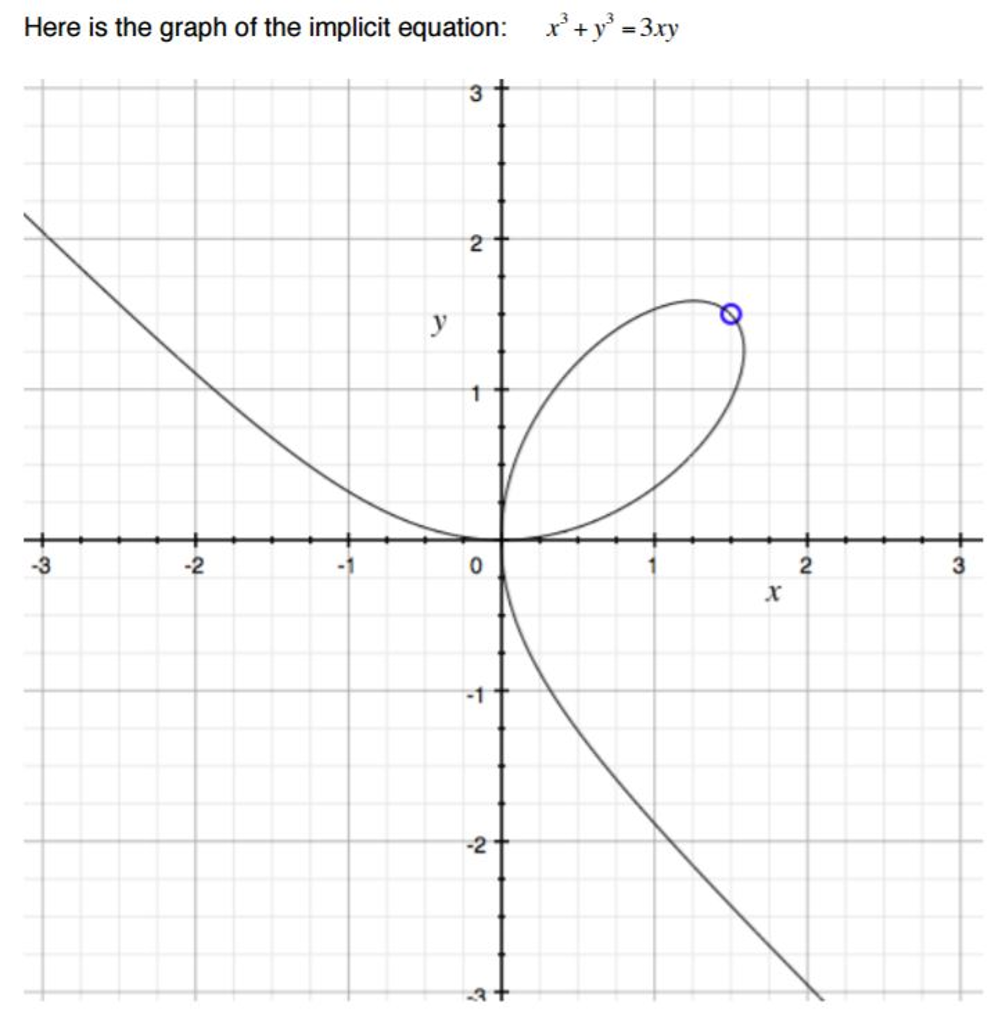



Here Is The Graph Of The Implicit Equation X 3 Y 3 Chegg Com



Www Assignmentexpert Com Homework Answers Mathematics Answer Pdf




How To Evaluate Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




The Solution Of X Y 3 Dx 3xy 2 Dy 0 Is



1
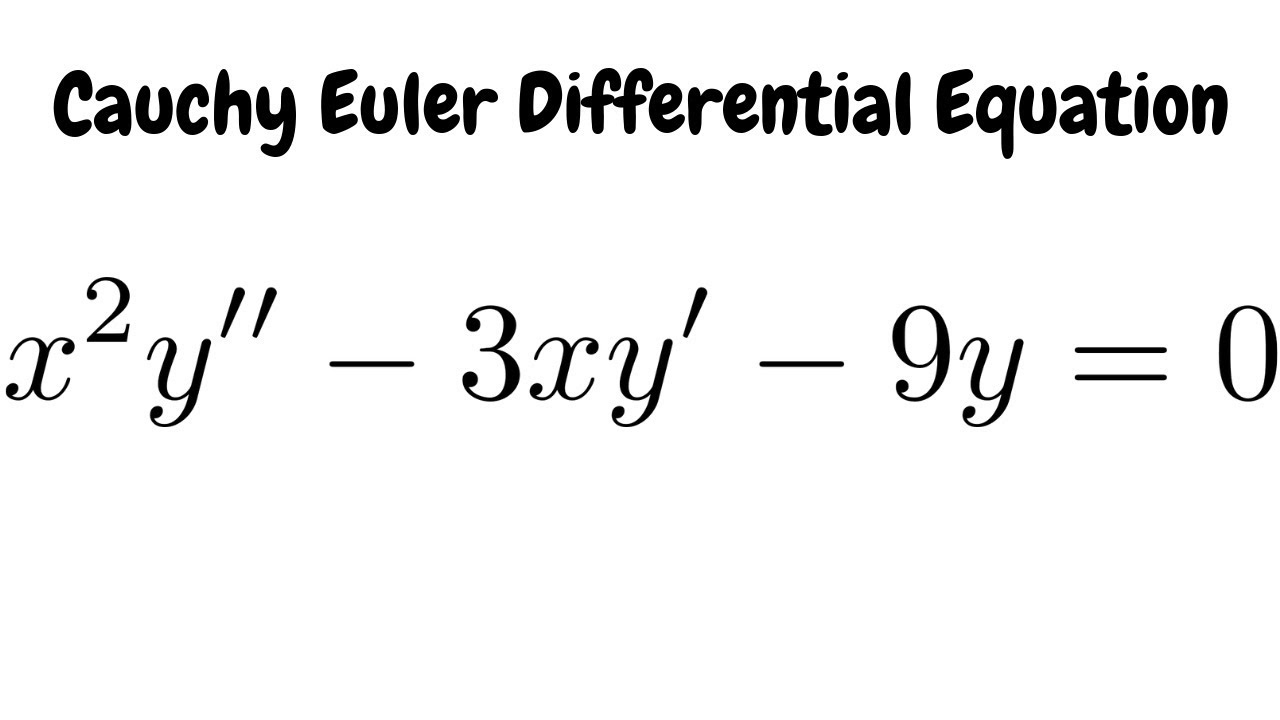



Solve X 2y 3xy 9y 0 Cauchy Euler Differential Equation Youtube




Solve Differential Equation X 3 3xy 2 Dx Y 3 3x 2y Dy Maths Differential Equations Meritnation Com



K 6y Y 1 7y 7y M 3x 4x N 6x X 0 2y 5 Gauthmath




Answers
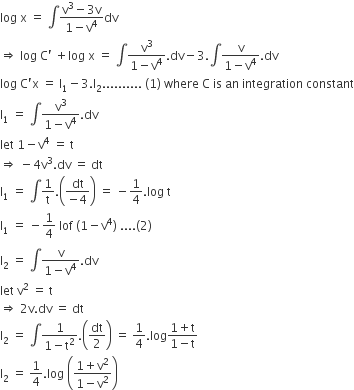



Prove That X2 Y2 C X2 Y2 2 Is The General Solution Of The Differential Equation X3 3xy2 Dx Y3 3x2y Dy Where C Is A Parameter From Class




Ppt Polynomials Powerpoint Presentation Free Download Id



Divide The Given Polynomials By Monomials X2y 3xy By Xy Snapsolve




3 A Find All Asymptotes Of See How To Solve It At Qanda




Factoring Two Variable Quadratics Rearranging Video Khan Academy



Find The Extreme Values Of The Function X 3 Y 3 3xy Sarthaks Econnect Largest Online Education Community




University Calculus Elements With Early Transcendentals 1st Edition H



X 3 Y 3 3xy 2 Find Dy Dx Using Implicit Differentiation Youtube




Let F X Y X 3 3xy 2 2y 3 Show That The Chegg Com




Solved Find And Identify The Critical Points Of Z X 3 3xy 2 3x 2 3y 2 7




X 3 Y 3 Z 3 Novocom Top




Consider The Function F X Y X 3 Y 3 3xy Chegg Com



What Should Be Added To X2 Xy Y2 To Obtain 2x2 3xy Algebraic Expressions Maths Class 7



The Two Curves X 3 3xy 2 2 0 And 3x 2y Y 3 2 0 Youtube



If Math X 3 Y 3 3xy 1 Math What Is The Minimum Value Of Math X 2 Y 2 Math Quora




X 9y 3xy X Y Answer It Plz With Full Maths Brainly In




X 3 3xy 2 Dx Y 3 3x 2y Dy Youtube



If X Y 2 Then What Is The Value Of X Y 6xy Quora




X 9y 3xy X Y Answer It Plz With Full Maths Brainly In




Analyze The Product Of X 3 9y 3 3xy X Y



1




Factorise X Y 3 X 3 Y 3 3xy X Y Brainly In



Search Q X Y 5e3 Formula Tbm Isch
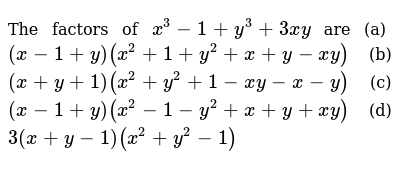



The Factors Of X 3 1 Y 3 3x Y Are A X 1 Y X 2 1 Y 2 X Y




If X 3 Y 2 3xy X Y Then Log X Y 3




Solve X 3 2y 3 Dx 3xy 2dy 0



If A Line Y 3 X Cuts The Curve X 3 Y 3 3xy 5x 2 3y 2 4x 5y 1 0 At The Points A B And C
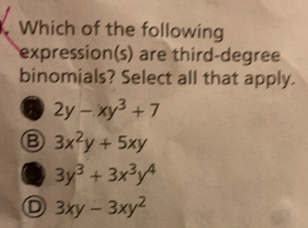



Which Of The Following Expression S Are Third Degree Binomials Select All That Apply A Math 2y Xy 3 7 Math B Math 3x Y 5xy Math C Math 3y 3 3x 3y 4 Math D Math 3xy 3xy 2 Math Homework Help And Answers Slader




X X3 Y3 3xy X Y Brainly In




The Factors Of X 3 1 Y 3 3x Y Are A X 1 Y X 2 1 Y 2 X Y




X3 9y3 3xy X Y এর উৎপ দক ব শ ল ষণ কর Brainly In
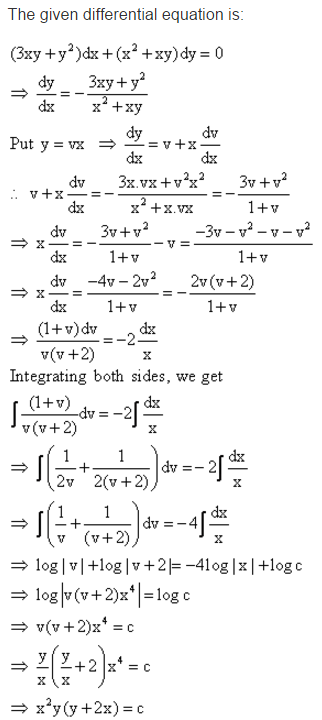



Find The Particular Solution Of Given Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 At X 1 Y 1 Mathematics Topperlearning Com D1ksg633




X Y 3 X 3 Y 3 3xy X Y Verify Maths Meritnation Com
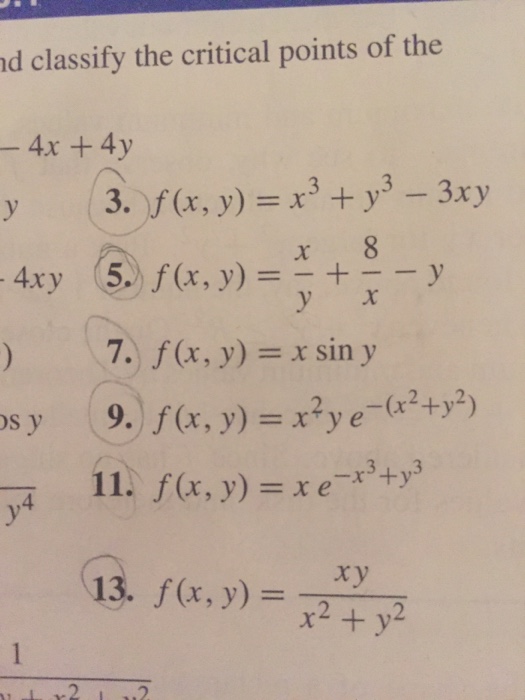



D Classify The Critical Points Of The 4x 4y Y 4m Chegg Com




If X 3 Y 2 3xy X Y Then Log X Y 3




If X 3 Y 3 3xy 2 3x 2y 1 0 Then At 0 1 Dy Dx Youtube




If X 3 Y 3 1 3xy Where X Y Determine The Value Of X Y 1
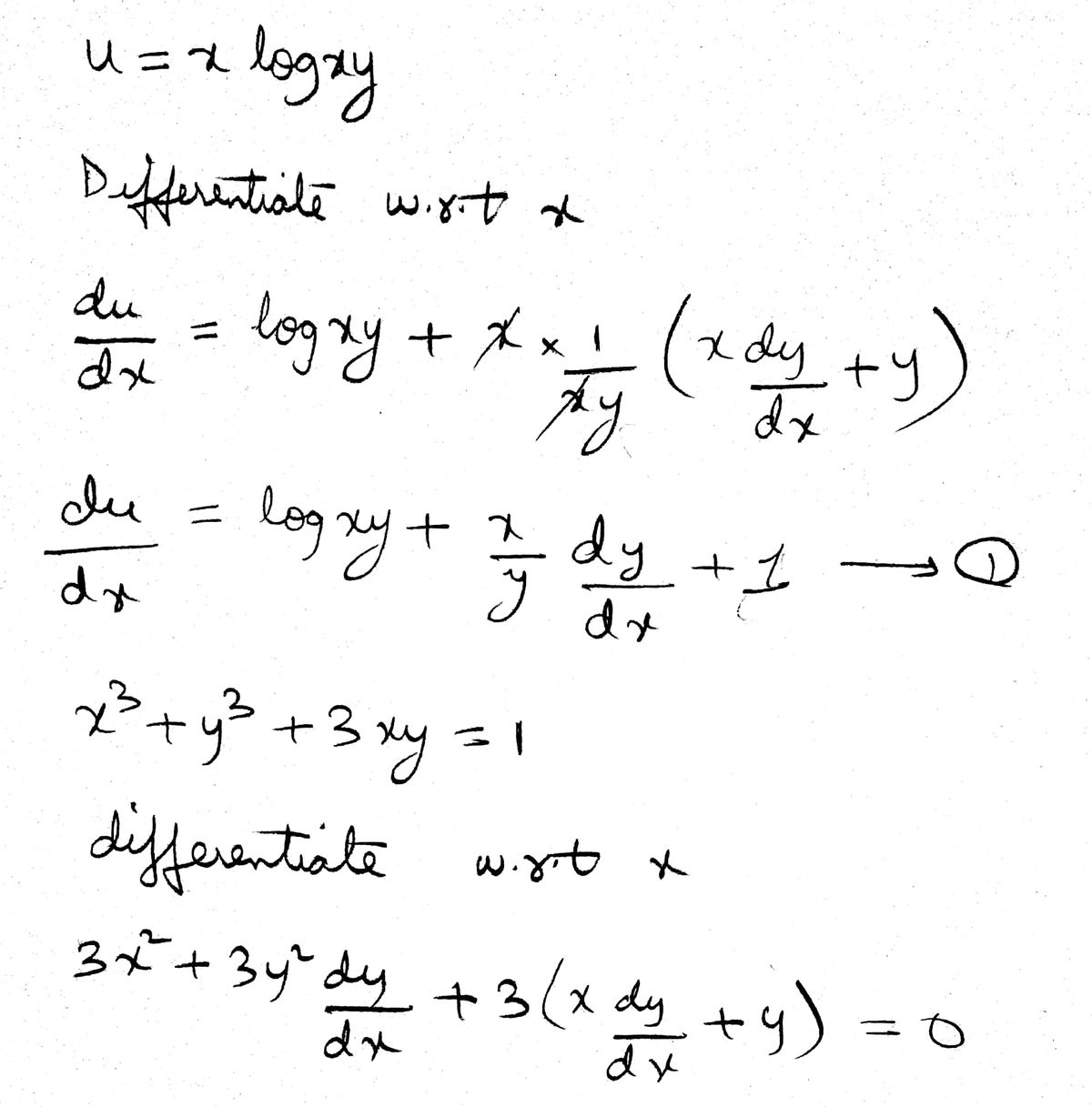



Answered If U X Log Xy Where X3 Y3 3xy 1 Find Bartleby
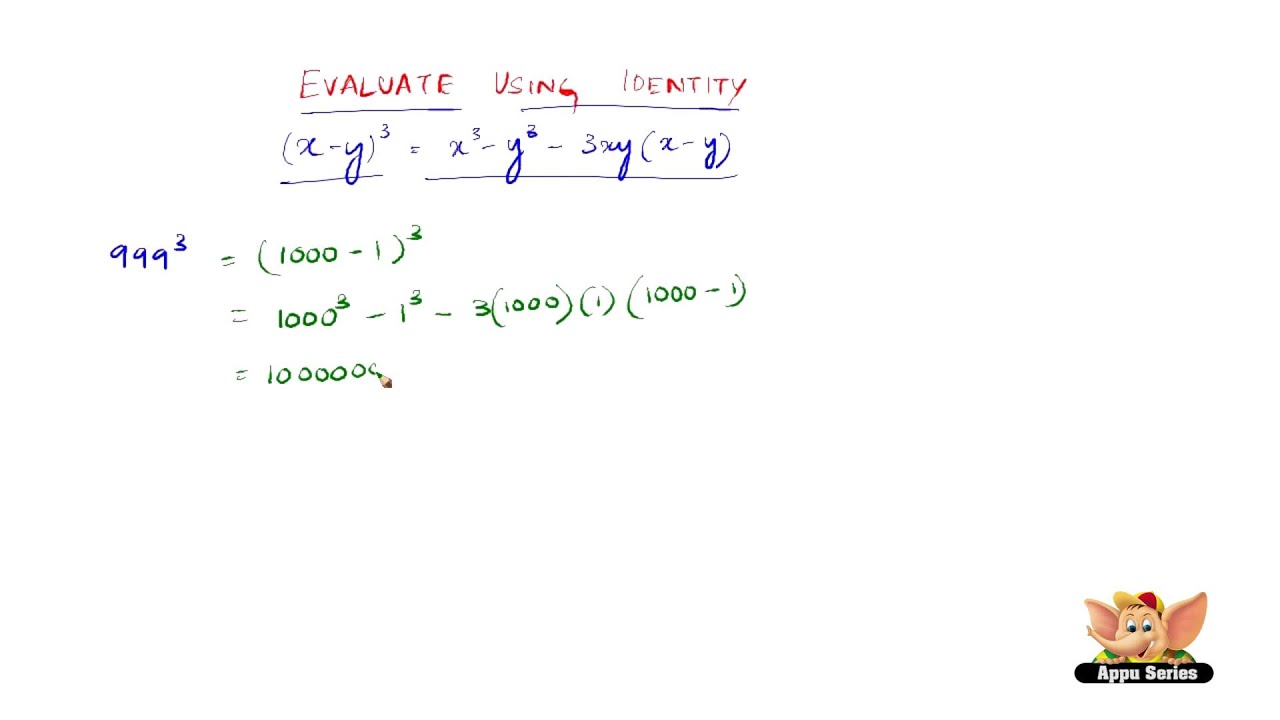



How To Evaluate Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Solve The Exact Differential Equation X 3 Y 3 Dx Chegg Com




How To Factorise Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Ntity Sqrtt Xy 3x3y33xy Xy See How To Solve It At Qanda




How To Solve 3xy Y 2 Dx X 2 Xy Dy 0 Also I Wish To Knw When To Use Y Vx Or X Vy Mathematics Topperlearning Com H9faf2xx




Bamo Aftermath And Aime Prep Berkeley Math Circle




X X3 Y3 3xy X Y Maths Polynomials Meritnation Com



Factorize X X 3 Y 3 3xy X Y Sarthaks Econnect Largest Online Education Community




Ex 12 2 4 A What Should Be Added To X 2 Xy Y 2 To Obtain




3 A Classify Each Ode By Order And Linearity Y 3xy Xy 0 Homeworklib




Factorise X X3 Y3 3xy X Y Brainly In




Factorise X3 9y3 3xy X Y Brainly In
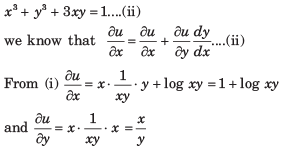



If U X Log Xy Wherex3 Y3 3xy 1 Then Du Dx Is Equal Toa B C D Correct Answer Is Option A Can You Explain This Answer Edurev Electronics And Communication Engineering Ece




Verify X Y 3 X3 Y3 3xy X Y Brainly In



0 件のコメント:
コメントを投稿