f(x) = x 3 6x 2 11x 6 and g(x) = x 1 Clearly, degree of f(x) = 3 and degree of g(x) = 1 Therefore, the degree of quotient is q(x) = 3 1 = 2 and the degree of remainder is r(x) = 0 Let quotient q(x) = ax 2 bx c and remainder r(x) = k Using division algorithm, we have f(x) = g(x) × q(x) r(x)Simple and best practice solution for (x6)(x7)=(x3)(x11) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itIt is given that f(x) = x 3 − 6x 2 11x − 6, and g(x) = x 2 − 3x 2 We have g(x) = x 2 − 3x 2 ` = x^2 2x x 2` ` = (x 2) (x1)` \\Rightarrow \left( x 2 \right)\ and (x − 1) are factor of g(x) by the factor theorem
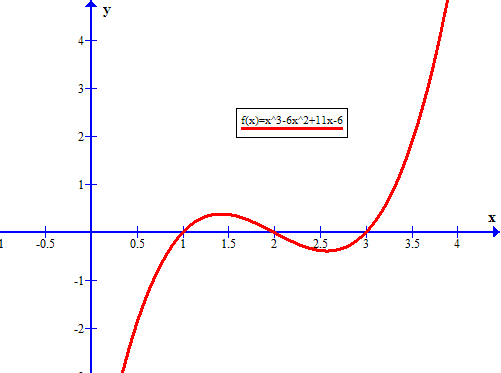
How Do You Use The Graph Of F X X 3 6x 2 11x 6 To Rewrite F X As A Product Of Linear Factors Socratic
F(x)=x^3-6x^2 11x-6 g(x)=x^2 x 1
F(x)=x^3-6x^2 11x-6 g(x)=x^2 x 1- If x^36x^211x6 is a prime number then number of possible integral values of x is Updated On 214 To keep watching this video solution for FREE, Download our App Join the 2 Crores Student community now! A quadratic function has a vertex at the point (4, 2) and passes through the point (8,6) Part D Identify how you see the x and yintercepts and the vertex in the table, graph, and equation (Hint You may want to rewrite the equation in equivalent forms)
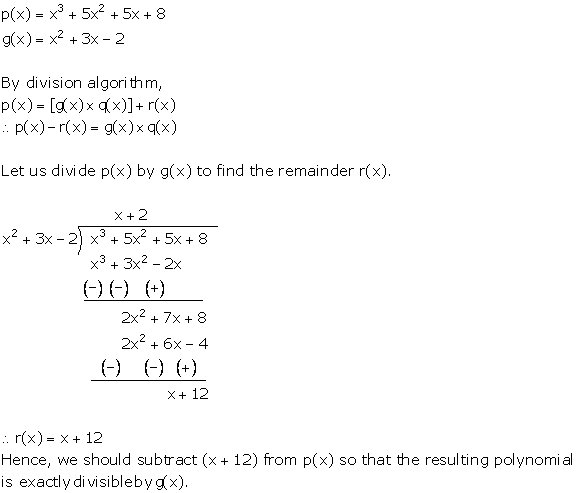



Chapter 8 Polynomials Government Of Karnataka Solutions For Class 10 Mathematics Maharashtra Topperlearning
Factoring by pulling out fails The groups have no common factor and can not be added up to form a multiplication Polynomial Roots Calculator 54 Find roots (zeroes) of F(x) = x 5 6x 4 11x 3 6 1 let f(x)=5x4 and g(x)=6x7 find f(x)g(x) A 11x3 B x3 C 11x11 D x11 2 let f(x)=3x2 and g(x)=6x7 find f(x)g(x) A 3x9 B 3x9 C 3x5 D 2x1 3 let f(x)=53 and g(x)=6x2 find f*g and its domain A 30x^228x6; x^3 6x^211x 6 I want to factorize it what are easiest and quicktest way to find the factors ?
Exercise 64 Page No 624 In each of the following, use factor theorem to find whether polynomial g (x) is a factor of polynomial f (x) or, not (17) Question 1 f (x) = x3 – 6x2 11x – 6;Algebra Calculator get free stepbystep solutions for your algebra math problems Example 2 Using factor theorem, factorize the polynomial x 3 – 6x 2 11 x – 6 Solution Let f (x) = x 3 – 6x 2 11x – 6 The constant term in f (x) is equal to – 6 and factors of – 6 are ±1, ± 2, ± 3, ± 6 Putting x = 1 in f (x), we have f (1) = 1 3 – 6 ×1 2 11× 1– 6 = 1 – 6 11– 6 = 0 ∴ (x– 1) is a
Group 1 11x 3 6 Group 2 x 5 6x 4 Pull out from each group separately Group 1 (11x 3 6) • (1) Group 2 (x 6) • (x 4) Bad news !!F(x) = x^3−2x^2−11x+12 Extended Keyboard;A h(x) = 12 11x 2 B h(x) = x2 – 11x2 C h(x) = x2 x – 4 D h(x) = 3r2 x – 4 E h(x) = x2 x2 Categories Mathematics Leave a Reply Cancel reply Your email address will not be published Required fields are marked * Comment



Efisd Net Common Pages Displayfile Aspx Itemid



1
Factorx^{3}6x^{2}11x6 he Related Symbolab blog posts Practice Makes Perfect Learning math takes practice, lots of practice Just like running, it takes practice andLet f(x) = x^3 6x^2 11x 6 Try x = 1: f(1) = 1 6 11 6 = 0 So x 1 is a factot of f(x) Try x = 2: f(2) = 8 24 22 6 = 0 x^16 4 x^15 10 x^14 x^13 35 x^12 52 x^11 68 x^10 80 x^9 85 x^8 80 x^7 68 x^6 52 x^5 35 x^4 x^3 10 x^2 4 x 1 The answer to the last question is CPhill




2




Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver
This video shows an example of graphing a polynomial function with a highest degree that is oddAll real numbers except x=1/3 B 15x^28x12; The sum of the values of a for which $$\frac{x^36x^211x6}{x^3x^210x8} \frac a{30} = 0$$ does not have a real solution is A $1$ B $12$ C $13$ D $2$ I tried to factorise the numerator and




Module 2 Polynomial Functions



Q Tbn And9gcqotbl1r9rl9mwpeeu1fvks6bkssuyw2uqurh Ff1sgjbpszu4h Usqp Cau
611x6x^2x^3=0 2x^5x^42x1=0 116xx^2=\frac {6} {x} x^32x=0 2x^5x^42x1=0 polynomialequationcalculator 611x6x^2x^3=0You can put this solution on YOUR website!3 is a zero 3 1 1 10 6 3 12 6 1 4 2 0 So we have factored f(x) as Now we must factor into two linear factors We find its zeros by setting it equal to 0 so the other two zeros are and So the remaining linear factors are and EdwinClick here👆to get an answer to your question ️ Divide x^3 6x^2 11x 6 by x^2 x 1




Find The Remainder When P X 6x2 14x 3 Is Divided By Gor Scholr



How To Factorise X 3 6x 2 11x 6 0 Youtube
x^36x^211x6=color(red)((x1)(x2)(x3)) There are several ways to approach this One of the most reliable is to hope that the expression has rational roots and apply the Rational Root Theorem In this case, the Rational Root Theorem tells us that (if the expression has rational roots) those roots are integer factors of 6 (the constant term of the expression) F(x) = 2×2 – 5x3 8(x) = x2 6x1 What is h(x) if h(x) = g(x)f(x)?F(x) = x 3 − 6x 2 11x − 6 g(x) = x 2 x 1 Here, degree f(x) = 3 and Degree (g(x)) = 2 Therefore, quotient q(x) is of degree 3 2 = 1 and the remainder r(x) is of degree less than 2 Let q(x) = ax b and r(x) = cx d Using division algorithm, we have f(x) = g(x) x q(x) r(x) x 3 − 6x 2 11x − 6 = (x 2 x 1)(ax b




2




Answered 19 F X X 2 2 4 X 1 3 3 3 Bartleby
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `x^36x^211x6=0`Find stepbystep Engineering solutions and your answer to the following textbook question Determine the highest real root of $$ f(x) = x^3 6x^2 11x 61 $$ (a) Graphically (b) Using the NewtonRaphson method (three iterations, $$ x_i = 35 $$ ) (c) Using the secant method (three iterations, $$ x_{i1}= 25 $$ and $$ x_i = 35 $$ ) বহুবর্ষীয় এফ (এক্স) = x ^ 3 6x ^ 2 11x 6 এর অবিচ্ছেদ্য শিকড় খুঁজে 306k



Http Smacmathapcalculus Weebly Com Uploads 1 9 2 5 Fc Unit 3 1 Hw Key V2 Pdf



2
Question Given f(x)=x^36x^211x6 Show that f(2)=0 and find the three factors of f(x) Found 2 solutions by CharlesG2, ewatrrrThe Algebra of Functions Like terms, functions may be combined by addition, subtraction, multiplication or division Example 1 Given f ( x ) = 2x 1 and g ( x ) = x2 2x – 1 find ( f g ) ( x ) and ( f g ) ( 2 )23 Find roots (zeroes) of F(x) = x 3 6x 2 11x 6 Polynomial Roots Calculator is a set of methods aimed at finding values of x for which F(x)=0 Rational Roots Test is one of the above mentioned tools It would only find Rational Roots that is numbers x which can be expressed as the quotient of two integers



How Would We Solve The Equation X 3 6x 2 11x 6 0 Quora




Apply Division Algorithm To Find The Quotient Q X And Remainder R X Obtaimed On Dividing X3 6x2 11x 6 By X2 X 1 Ate I And 2 Maths Polynomials Meritnation Com
Explanation Rolle's theorem states that if a function f (x) is continuous on the interval a,b and differentiable on the interval (a,b) and if f (a) = f (b) then there exists c ∈ (a,b) such that f '(c) = 0 Here, f (x) = x3 − 6x2 11x −6 The interval is I = (1,3) f (1) = 13 − 6 × 12 11 × 1 −6 = 0 f (3) = 33 − 6 × 32 11 × 3 −6 = 0All real numbers except x=3/5 C 30x^228x6; Factorise The given Polynomial Find what must be subtracted from 4y412y36y250y26 so that obtained polynomial is exactly divisible by y24y2 Factorise 2u33u217u30 Using factor theorem factorise the polynomial x rays to 4 x rays to 3 7x rays to 2 x 6 Find integral zeros of 2xcube 3xsquare 8x12




Fx X3 6x2 11x 6 Gx X 3 Fx 2x3 9x2 X 12 Gx X Gauthmath




Solve The Following Equations X 3 6x 2 11x 6 6
Determine the highest real root of (x) = x 3 6x 2 11x 61 (a) Graphically (b) Using the NewtonRaphson method (three iterations, x 0 = 35 (c) Using the secant method (three iterations, r 1 = 25 and x 0 = 35) (d) Using the modified secant method (three iterations, x 0 = 35, δ = 001) (e) Determine all the roots with MATLASSubtract 6 6 from 1 1 Multiply 11 11 by 1 1 Add − 5 5 and 11 11 Subtract 6 6 from 6 6 Since 1 1 is a known root, divide the polynomial by x − 1 x 1 to find the quotient polynomial This polynomial can then be used to find the remaining roots Divide x 3 − 6 x 2 11 x − 6 x 3 6 x 2 11 x 6 by x − 1 x 1Graph f(x)=x^36x^211x6 Find the point at Tap for more steps Replace the variable with in the expression Simplify the result Tap for more steps Simplify each term Tap for more steps Raising to any positive power yields Raising to any positive power yields Multiply by




Divide The Polynomial X3 6x2 11x 6 By X 3 And Check Whether X 3 Is A Factor Of The Polynomial Brainly In



1
In each of the following, g(x) is a factor of polynomial f(x) or, not f(x) = x^3 6x^2 11x 6, g(x) = x^2 3x 2 asked Apr in Polynomials by Daivi ( In each of the following, g(x) is a factor of polynomial f(x) or, not f(x) = x^3 6x^2 11x 6, g(x) = x^2 3x 2 asked Apr in Polynomials by Daivi (The equation is in standard form xf=x^ {3}4x^ {2}11x30 x f = x 3 − 4 x 2 − 1 1 x 3 0 Divide both sides by x Divide both sides by x \frac {xf} {x}=\frac {\left (x5\right)\left (x2\right)\left (x3\right)} {x} x x f = x ( x − 5) ( x − 2) ( x 3) Dividing by x undoes the multiplication by x



Http Math Arizona Edu Cjewell 122b Handouts Derivativepractice Pdf




Solving Cubic Equations Solutions Examples Videos
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicClick here👆to get an answer to your question ️ Divide x^3 6x^2 11x 6 by x 2 and verify the division algorithmCalculadoras gratuitas paso por paso para álgebra, Trigonometría y cálculo



F X X 3 6x 2 11x 6 G X X 2 X 1 Sarthaks Econnect Largest Online Education Community
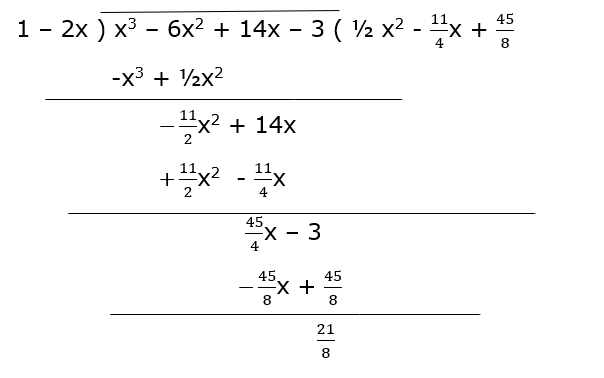



Ex 2 3 Q8 Find The Remainder When P X X 3 6x 2 14x 3 Is Divided By G X 1 2x
Calculadoras gratuitas passo a passo para álgebra, trigonometria e cálculoG (x) = x – 3 Solution If g (x) is a factor of f (x), then the remainder will be zero that is g (x) = 0 Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 32 Question 1 Note that 3 is not a divisor of g (x) Now dividing g (x) = x 3 x 2 – 5x 3 by the new remainder x 2 2x – 3 (leaving the constant factor 3) we get Question 2




Simplify If Fx Frac X2 2x 3x2 3x 4 And Gx Frac 3 Gauthmath



Www Npsd K12 Nj Us Cms Lib04 Nj Centricity Domain 156 2 3 the remainder and factor theorems Pdf
How do you factor x^3 6x^2 11x 6 = 0 ?Solution Steps g ( x ) = x ^ { 3 } 2 x ^ { 2 } 11 x 6 g ( x) = x 3 − 2 x 2 − 1 1 x − 6 By Rational Root Theorem, all rational roots of a polynomial are in the form \frac {p} {q}, where p divides the constant term 6 and q divides the leading coefficient 1 One such root is 2 Factor the polynomial by dividing it by x2By inspection, x = 1 is a zero so (x1) is a factor By synthetic division x^3 6x^2 11x 6 = 0 → (x 1)(x^2 5x 6) = 0 For the quadratic factor 6 = 2*3 → 23 = 5 The quadratic factors nicely




2 4 Zeros Of Polynomial Functions 1 7 Find All The Chegg Com



Www Jensenmath Ca Unit 2 review factoring solutions Pdf
Homework 5 Solutions x42 #1 d Use the division algorithm to find the quotient and remainder when f(x) = 2x4 x3 6x2 x2 is divided by g(x) = 2x2 5 over Q Solution Long division gives F(x)=x^36x^211x6,g(x)=x^2x1 2 See answers jyotikadam177 jyotikadam177 write full question I don't understand you write first full question then I will give you answer Kripatomar Kripatomar AnswerSimple and best practice solution for g(x)=2x^35x^211x14 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework



Www Lcps Org Cms Lib4 Va Centricity Domain 4777 Test key unit 5 Pdf




Divide The Polynomial X3 6x2 11x 6 By X 3 And Check Whether X 3 Is A Factor Of The Polynomial Brainly In
The factors are 1, 2, and 3 Stepbystep explanation According to Factor theorem, if (x a) is a polynomial factor f(x), then f(a) = 0 Let Let us check if (x 1) is the factor of f(x), Then, Therefore (x1) is a factor of f(x) Let us check for the other factors Hence, Therefore, 1, 2, 3 are the factors of f(x)Question 11 What must be added to the polynomial f(x) = x 4 2x 3 – 2x 2 x − 1 so that the resulting polynomial is exactly divisible by g(x) = x 2 2x − 3 Solution f(x) = x 4 2x 3 – 2x 2 x − 1 We must add (x – 2) in order to get the resulting polynomial exactly divisible by g(x) = x 2 2x − 3




F X X 3 6x 2 11x 6g X X 2 Brainly In




Finding All Solutions Of Polynomial Functions Ck 12 Foundation




Finding Zeros Of Polynomials 2 Of 2 Video Khan Academy




Rd Sharma Class 10 Solutions Maths Chapter 2 Polynomials Exercise 2 3



Www Mpsaz Org Rmhs Staff Esritter Algebra2 Files Ch 1 2 Review Key Pdf




Factorize X 3 6x 2 11x 6 Youtube




X 3 6x 2 11x 6 0 Youtube



Www3 Nd Edu Apilking Math Work Old exams Exam1f08soluutions Pdf




Class 10 Rd Sharma Solutions Chapter 2 Polynomials Exercise 2 3 Geeksforgeeks




How Do You Use The Graph Of F X X 3 6x 2 11x 6 To Rewrite F X As A Product Of Linear Factors Socratic
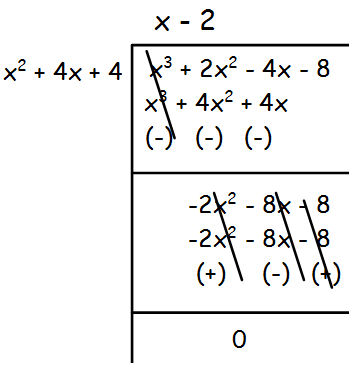



Gcd Of Polynomials Using Division Algorithm



Mathscene Factorising Polynomials Lesson 1




Apply Division Algorithm To Find The Quotient Q X And Remainder R X Obtaimed On Dividing X3 6x2 11x 6 By X2 X 1 Ate I And 2 Maths Polynomials Meritnation Com
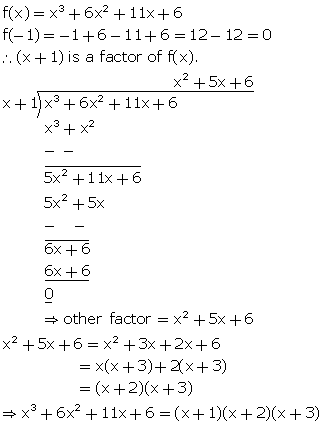



Factorize X3 6x2 11x 6 Mathematics Topperlearning Com Iv3dg99oo




Chapter 2 Problems




Solved Determine The Highest Real Root Of F X X 3 6x 2 11x 6 1 1 Answer Transtutors
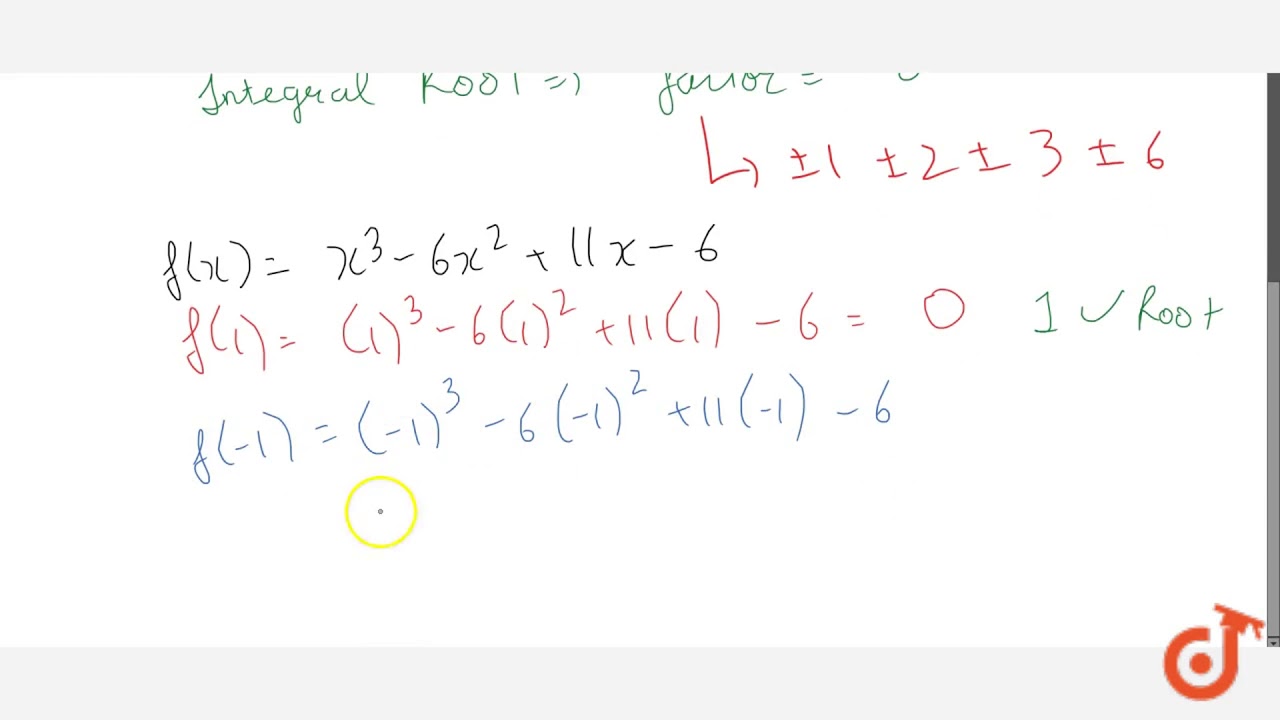



Find Integral Roots Of The Polynomial X 3 6x 2 11x 6 Youtube




Rd Sharma Class 9 Solutions Maths Updated For 21 22 Chapter 6 Factorization Of Polynomials




How To Factor Math X 4 X 3 7x 2 X 6 Math Quora



Www Wsfcs K12 Nc Us Cms Lib Nc Centricity Domain 8543 Math iii polynomial review key Pdf




Focus In High School Mathematics Reasoning And Sense Making Pdfdrive Com Flip Book Pages 51 100 Pubhtml5
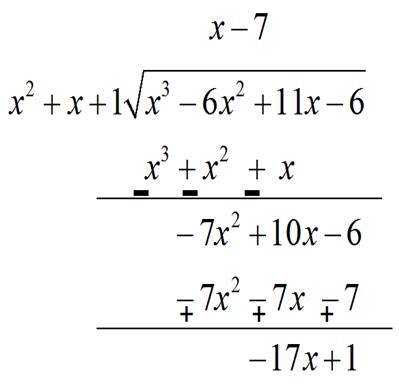



Apply Division Algorithm To Find The Quotient Q X And Remainder R X On Dividing F X By G X Where F X X 3 6x 2 11x 6 And G X X 2 X 1 Snapsolve



View Question Just A Few Questions




How To Factor Math X 3 6x 2 11x 6 0 Math Quora



Solved This Is An Algebra 2 Question One Factor Of The Function F X X3 6x2 11x 6 Is X 3 Describe How To Find The X Intercepts And The Y Int Course Hero



Efisd Net Common Pages Displayfile Aspx Itemid
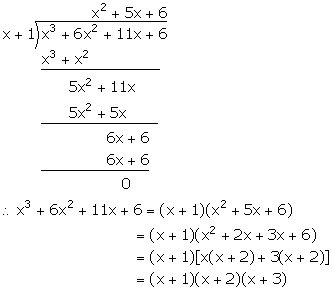



Chapter 8 Remainder And Factor Theorems Selina Concise Mathematics Part Ii Solutions For Class 10 Mathematics Icse Topperlearning




F X X 3 6x 2 11x 6 G X X 2 Brainly In




Ex 2 4 2 Use The Factor Theorem To Determine Whether Ex 2 4




In Each Of The Following Use Factor Theorem To Find Whether Polynomial G X Is A Factor Of Polynomial F X Or Not F X X 3 6x 2 11x 6 G X



Search Q X3 6x2 2b11x 6 Divided By X 2b2 Tbm Isch




Divide X 3 6x 2 11x 6 By X 2 X 1
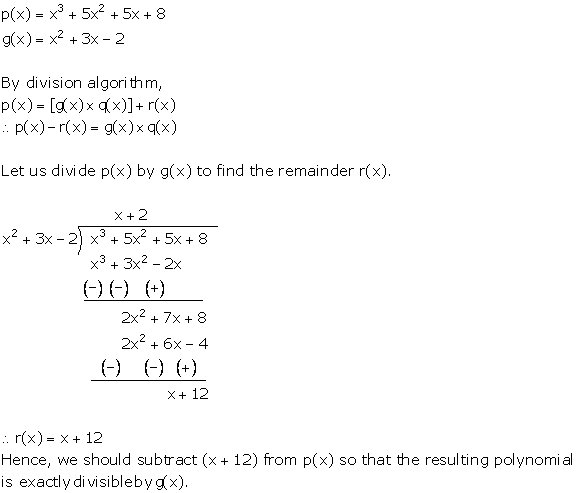



Chapter 8 Polynomials Government Of Karnataka Solutions For Class 10 Mathematics Maharashtra Topperlearning



Www Sgasd Org Site Handlers Filedownload Ashx Moduleinstanceid 9221 Dataid Filename Answer key Pdf



By Remainder Theorem Find The Remainder When P X Is Divided By G X Studyrankersonline




Factor Factor A Polynomial And Trinomial With Step By Step Math Problem Solver



Http Www Mpsaz Org Rmhs Staff Lxcoleman Trig Test Practice Files Review Chapter 3 Notes Solutions Pdf



2




Compute The Derivative Of The Given Function F X Chegg Com
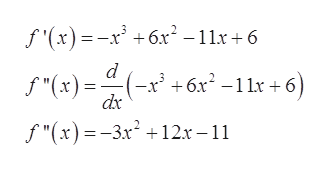



Answered Suppose That C 1 Is A Critical Number Bartleby



Http Petalschools Com Cms Lib03 Ms Centricity Domain 455 hw 8 3 Pdf



Factorise X 3 6x 2 11x 6 Completely Using Factor Theorem Sarthaks Econnect Largest Online Education Community




Factorization Of Polynomials Using Factor Theorem A Plus Topper



How Do I Use Long Division To Simplify 12x 3 11x 2 9x 18 4x 3 Socratic




Numerical Methods For The Root Finding Problem Pdf Free Download




Warm Up Exercises 1 What Is The Degree Of F X 8x 6 4x 5 3x 2 Solve X 2 2x 3 0 Answer 6 1 I 2 Ppt Download




7 3 1 Products And Factors Of Polynomials Products And Factors Of Polynomials Objectives Multiply And Factor Polynomials Use The Factor Theorem Ppt Download




How To Factorise A Polynomial By Splitting The Middle Term A Plus Topper



Ehsgiftedacademy Weebly Com Uploads 1 4 0 2 16 Honors Precalculus Summer Packet Answer Key 3 0 Pdf



Http Www Eastauroraschools Org Cms Lib Ny Centricity Domain 323 Midterm 2 answers Pdf




Answers




If F X X 2 4 X 3 6x 2 11x 6 X 1 X Then Set Of Points At Which The Function If Non Differentiable Is




Divide X 3 6x 2 11x 6 By X 2 And Verify The Division Algorithm
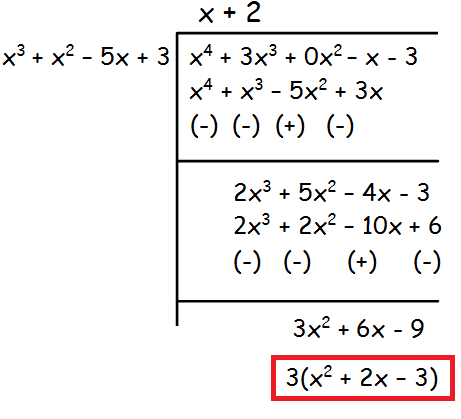



Gcd Of Polynomials Using Division Algorithm




F X X 3 6x 2 11x 6 G X X 3 Solve It Now For Using Factor Theorem Maths Polynomials Meritnation Com




38 If X 3 6x 2 11x 8 X 2 1 Find The Sum Of Possible Valu
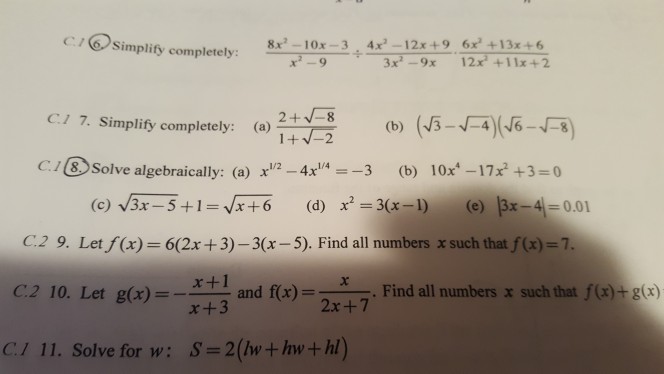



Simplify Completely 8x 2 10x 3 X 2 9 4x 2 Chegg Com




Finding Zeros Of Polynomials 2 Of 2 Video Khan Academy




Using Factor Theorem Show That G X Is A Factor Of P X When P X 2x 4 9x 3 6x 2 11x 6 G X X 1




In Exercises 21 Through 38 Differentiate The Given Function And Simplify Your Answer 21 F X 2 Homeworklib



Www Shakopee K12 Mn Us Cms Lib07 Mn Centricity Domain 280 Ch6 Solutions Pdf



P X X 3 6x 2 11x 6 G X X 2 5x 6 Sarthaks Econnect Largest Online Education Community



F X X 6x 11x 6 G X X X 1 Find The Quotient Sarthaks Econnect Largest Online Education Community
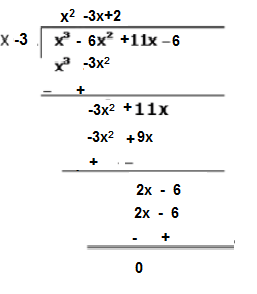



If One Zero Of The Polynomial P X X3 6x2 11x 6 Is 3 Find The Other Two Zeros Snapsolve



Uncw Edu Ulc Services Math Documents Mat 111 Final Exam Answer Key Sp17 Pdf




Apply Division Algorithm To Find The Quotient G X And Remainder R X An Dividing F X And G X Where Brainly In
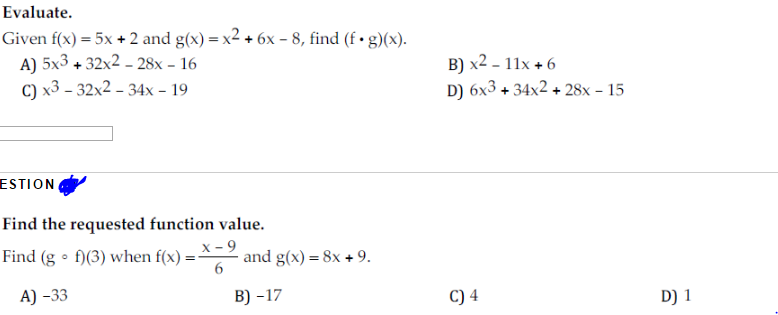



Given F X 5x 2 And G X X 2 6x 8 Find F Chegg Com
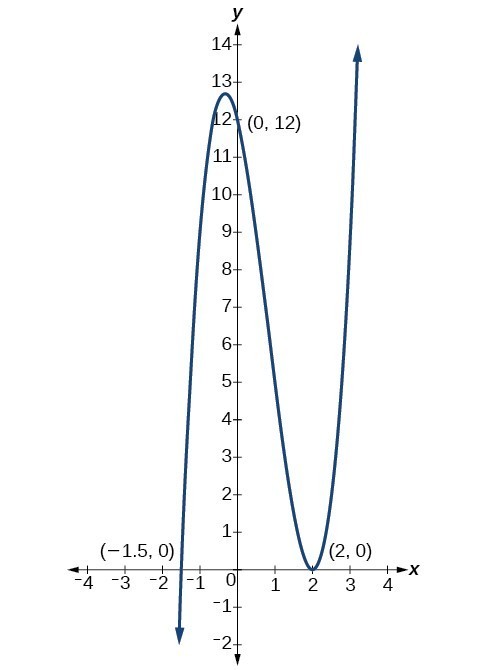



Use Factoring To find Zeros Of Polynomial Functions College Algebra



Mathscene Factorising Polynomials Lesson 1




X3 6x2 11x 6 Divided By X2 X 1 Brainly In




Examples Int 3x 2 X 3 6x 2 11x 6 Dx




Divide F X X3 6x2 11x 6 By G X X2 X 1 Using Division Algorithm Youtube




Module 1 Polynomial Functions




Polynomial Functions



It Is Given That X 2 5x 6 And X 3 6x 2 11x A Have A Common Factor What Is The Possible Value Of A Quora



How Do You Factor X 3 6x 2 11x 6 Socratic



0 件のコメント:
コメントを投稿