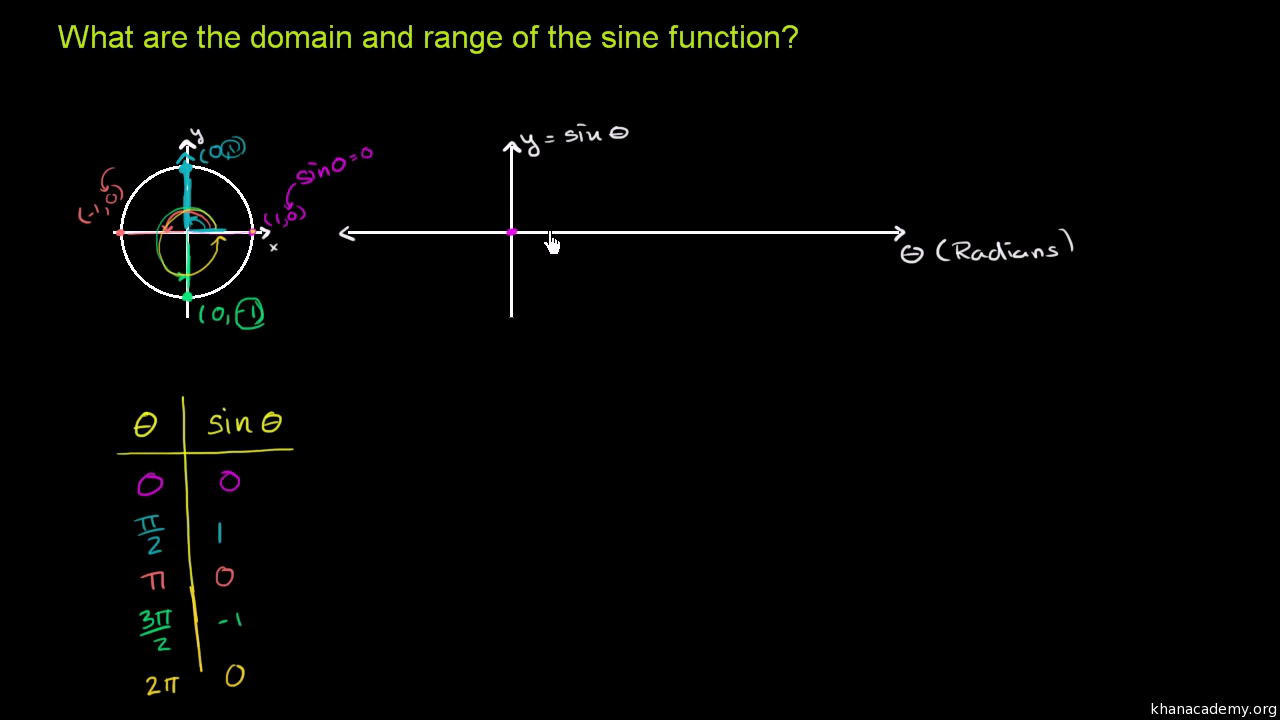
For example, in the function y = f(x) = 2x y, x is independent and y is dependent (in other words, y is a function of x) The valid values for a given independent variable x are collectively called the "domain" The valid values for a given dependent variable y are collectively called the "range" If a ticket costs 2 dollars, find the domain and range of this Precalculus The function f has a domain of 0,5and a range of 0,3 Start by sketching a potential graph of f Suppose the function k is defined as k(x)=f(x−3) Determine the domain and range of k Domain RangeSine The graph is periodic and repeats every 2Π I think this function should be familiar Domain All real numbers R, also written as (–∞,∞)We can input any real number Range The output from the "sine" function box (I'm sorry, I really do think this way!) is restricted to numbers between –1 and 1, including both endpoints So it is –1,1
Domain And Range Of A Function
Domain and range of f(x) = sin(x) – 5
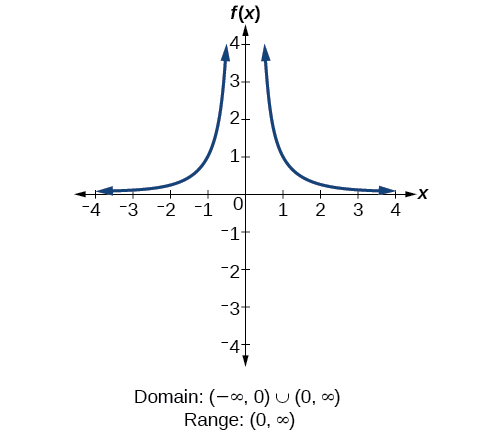
Domain and range of f(x) = sin(x) – 5-From the pictures above, it is very clear that the range of y = sin x and y = cos x is {y 1 ≤ y ≤ 1} Domain of csc x and sec x We know that sin (k π) = 0, cos (2k1) π /2 = 0, here "k" is an integer Then, k = 2, 1, 0, 1, 2, For k = 2, sin (2 π) = 0 and cos (3 π /2) = 0 For k = 1The domain of a function is any input that won't break it For example, the domain of f ( x) = 1 x − 3 is anything except x = 3 because division by zero is undefined ( − ∞, 3) ∪ ( 3, ∞) The range of a function is its outputs The range of f ( x) = 1 x − 3 is ( − ∞, 0) ∪ ( 0, ∞)




Domain And Range Of Trigonometric Functions
Example, if f(x) = sinx then the range is given by −1 ≤ f(x) ≤ 1 If we have a composed function gf then its range must lie within the range of the second function g Here is an example to show this Take domain is x 6= 0 , range is −2 ≤ y ≤ 2 wwwmathcentreacuk 5 c mathcentre 09Its domain and range can be found from the domain and range of sin(x) The csc( x ) cannot be defined for those values of x for which sin( x ) = 0 Its domain is all real numbers excluding x = 0TAP THE ARROWS BELOW TO ADVANCE f(x)=cos(x) Domain and Range (infinity,infinity) 1,1
Explanation The sine function is repetitive and continuous and bounded between 3 and 3 and so since domain is all possible input x values, these are all real numbers, and since range is all possible output y values, these are all real numbers between 3 and 3, both endpoints included Answer link Let f R R be defined by f(x) = 1 – x Then the range of f is (a) R (b) (1, ∞) (c) (1, ∞)What is domain and range?
Y = (2−sin 3x)1 ( 1 )Let f (x) = (2−sin 3x)1 Domain of f (x) is (−∞, ∞)From ( 1 ),2−sin 3x= y1 ⇒ sin 3x= 2− y1 ⇒ sin 3x = y2y −1 ⇒ 3x =sin−1( y2y −1 )⇒ x = 31 sin−1( y2y−1 ) ∵ y = 2−sin 3x1 ∴ y > 0as −1≤ sin 3x≤ 1 For x to be real−1 ≤ y2y−1 ≤1⇒ −y ≤ 2y−1≤ y y > 0 ⇒ 2y−1 ≥−y and 2y −1≤ y⇒ y ≥ 31 , y ≤The inverse function of f(x) = sin(x), x ∈ − π 2, π 2 is f − 1 = arcsin(x) We define arcsin(x) as follows y = arcsin(x) x = sin(y) where − 1 ≤ x ≤ 1 and − π 2 ≤ y ≤ π 2 Let us make a table of values of y = arcsin(x) and graph it along with y = sin(x), − π 2, π 2 x 1 0 1 y = arcsin(x) − π 2Find an answer to your question (9Q) Find the domain and range of f(x) = = 2x 3 3 sin x




Domain And Range Of Sin X And Its Inverse Youtube




The Domain Range Of Function F X Square Root Of Sinx 1 X Mathematics Topperlearning Com 437pco66
Range R Period ˇ Domain, Range, and De nition of the three main inverse trigonometric functions 1 sin 1(x) Domain 1;1 Range ˇ 2; The range of a function f (x) is the set of values f (x) lies in for x lying in the domain Here, and the domain is At x = and , At x = 0, sin x = 1 This gives the minimum value of f (x) as 1Arithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution Physics Mechanics domain\f(x)=\cos(2x5) domain\f(x)=\sin(3x) precalculusfunctiondomaincalculator en




Find The Domain And Range Of F X Sin 1 X X Where Represents The Greatest Integer Function




Find The Domain And Range Of The Function F X 1 2 Sin3x Youtube
Popular Problems Calculus Find the Domain and Range f (x)= (sin (x))/x f (x) = sin (x) x f ( x) = sin ( x) x Set the denominator in sin(x) x sin ( x) x equal to 0 0 to find where the expression is undefined x = 0 x = 0 The domain is all values of x x thatLet y = f(x) be a function Range is all real values of y for the given domain (real values of x) Let us look at some practice questions to understand how to find domain and range of a function Practice Questions Question 1 Find the domain of 1 / (1 − 2sinx) Solution 1 − 2sin x = 0 2sin x = 1 sin x = 1/2 sin x = sin π/6 Hence, both its domain and range should be real numbers x can be a number from –3 to 3 f(x) is between 0 & 3 Hence, Domain = Possible values of x = Any number from −3 to 3 = −3, 3 = {x −3 ≤ x ≤ 3} Range = Possible value of f(x) = Any number from 0 to 3 = 0, 3 = {x 0 ≤ x



Inverse Trigonometric Functions



3
f ( x) = ( 1 i f x = 0) or ( sin x x if x ≠ 0 ) where the domain is the set E = ( − ∞ ,0) ∪ (0, ∞ ) Answer The answer for the range is R = ( c, 1 where c = − cos x 0, such that x 0 is the smallest positive solution of x = tan Now, let us discuss the function f(x)= tan xF−1(x) = sin−1 x This inverse function is also written as arcsinx So, if the angle x lies in the range −90 ≤ x ≤ 90 and sinx = 3 4, we say x = sin−1(3 4) You can use your calculator to work out inverse sines Key Point The function f(x) = sinx has all real numbers in its domain, but its range is −1 ≤ sinx




The Graph Of The Function F X Sin X Is Shown What Is The Domain Of The Function Brainly Com



Www Alamo Edu Contentassets 35e1aad11a064ee2ae161ba2ae3b2559 Trigonometric Math2412 Inverse Trig Functions Pdf
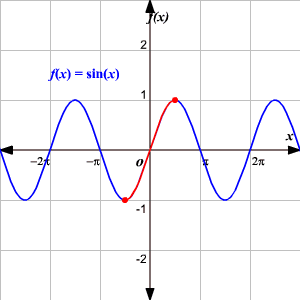
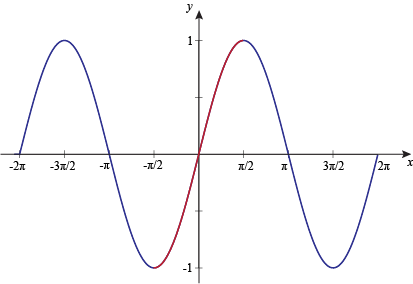
The domain of y = sin x is "all values of x", since there are no restrictions on the values for x (Put any number into the "sin" function in your calculator Any number should work, and will give you a final answer between −1 and 1) From the calculator experiment, and from observing the curve, we can see the range is y betweeen −1 and 1We could write this as −1 ≤ y ≤ 1If f is a function from set A to B and (a,b) ∈ f, then f(a) = b b is called the image of a under f and a is called preimage of b under f Summary Domain is defined as the entire set of values possible for independent variables The Range is found after substituting the possible x values to find the yvalues Video Lesson Related Threads on Find the domain and range of this function Find the domain and range of f(x)=10^(sinx)10^(cscx) Domain and range of composite function Last Post



Finding The Domain And Range Of A Function Graphically Expii




Domain And Range Of F X X 3 3x 2 x Sin X Are Respect
Domain and range graph The blue graph is the trigonometric function latexf(x)=sin (x)/latex with a domain of latex\mathbb{R}/latex and a restricted range of latex1 \leq y \leq 1/latex (output values only exist between latex1/latex to latex1/latex The red graph is the function latexf(x)=\sqrt{x}/latex with aFind the inverse of f(x)=(1/2x2)sq Determine whether it is function and state its domain and range asked in ALGEBRA 2 by payton Apprentice domainofafunctionFind the Domain and Range f (x)=sin (x) f (x) = sin(x) f ( x) = sin ( x) The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation



Graph Of Y Sin X Video Trigonometry Khan Academy




Find The Range Of F X Sin X Where Represents The Fractional Part Function And Youtube
Find the domain and range of the real function f (x) = x/1x^2 ━━━━━━━━━━━━━━━━━━━━━━━━━ ️Given real function is f (x) = x/1x^2 ️1 x^2 ≠ 0 ️x^2 ≠ 1 ️Domain x ∈ RFind the domain and range of {eq}g(x) = sin^{1} (3x 1) {/eq} Inverse Trigonometry arc sin In any inverse trigonometry function the argument within the inverse of sin has to be between 1Domain and Range of Sine Function y = f(x)= Sin(x) Range The value lies between 1 ≤ y ≤ 1 Domain It's determined for all the 'x' real values Period 2π = 360º Sine Function is an odd function The Graph of sin(x) function
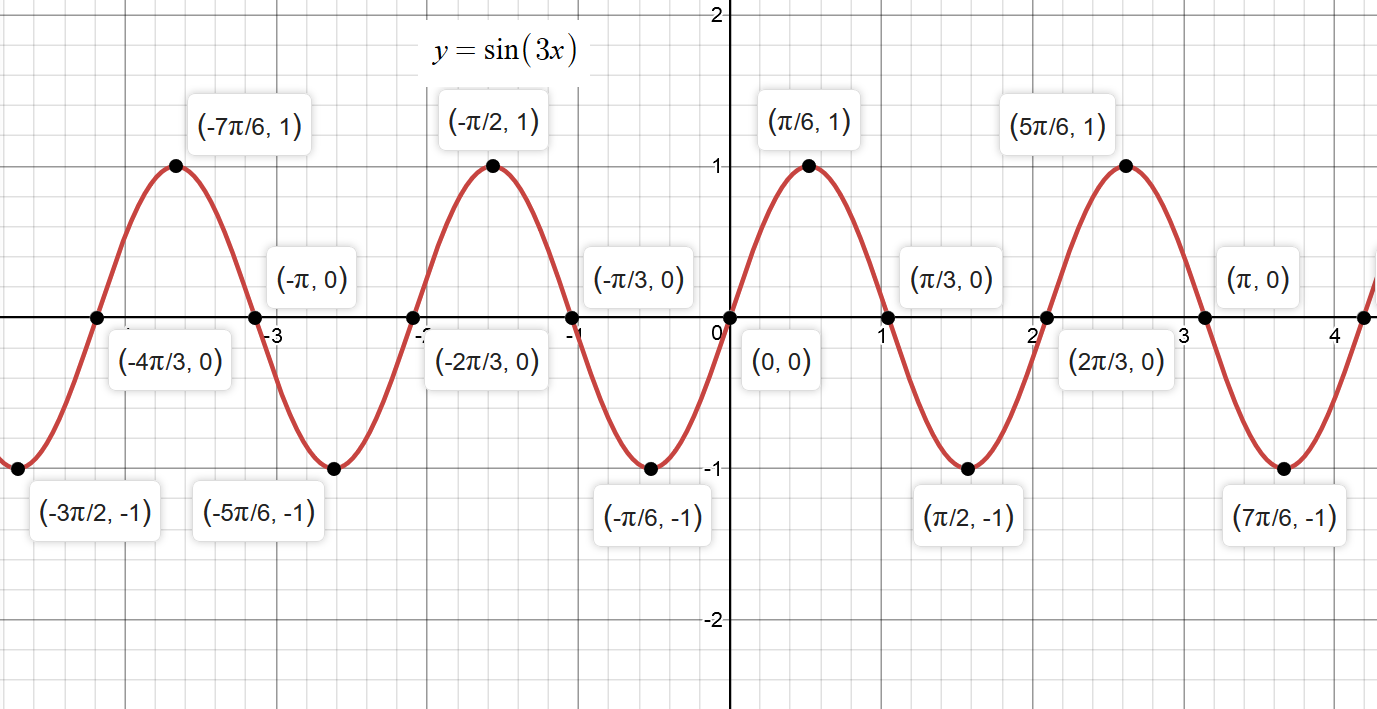



How Do You Graph Y Sin3x Socratic




14 1 Functions Of Several Variables Mathematics Libretexts
Given, f (x) = ∣ x − 1 ∣, f R → R and g (x) = e x, g (− 1, ∞) → R The function f o g ( x ) is defined, then its domain and range respectively are Hard ecuaciones trigonométricas en el intervalo 0°≤ x ≤ 360° 1) 4 cos2 x – 2 cos x 1 = 0 2) Sen2 x – 5 sen x 6 = 0 3)Cot2 x – 2 csc2 x 5 = 0 Dr Johnny Smith is looking up from camp at an angle of elevation of 27 degrees to the top of a Red Wood TreeSo, the maximum value of x = 2π/3 Whereas, the minimum value of x is 0 Therefore, the domain of the function, D f(x) = (0, 2π/3) Now, the minimum value of sinθ = 0 and the maximum value of sinθ = 1 So, the minimum value of the denominator is 1, and the maximum value of the denominator is 2 Therefore, the range of the function, R f(x




Domain And Range And Composition Of Functions
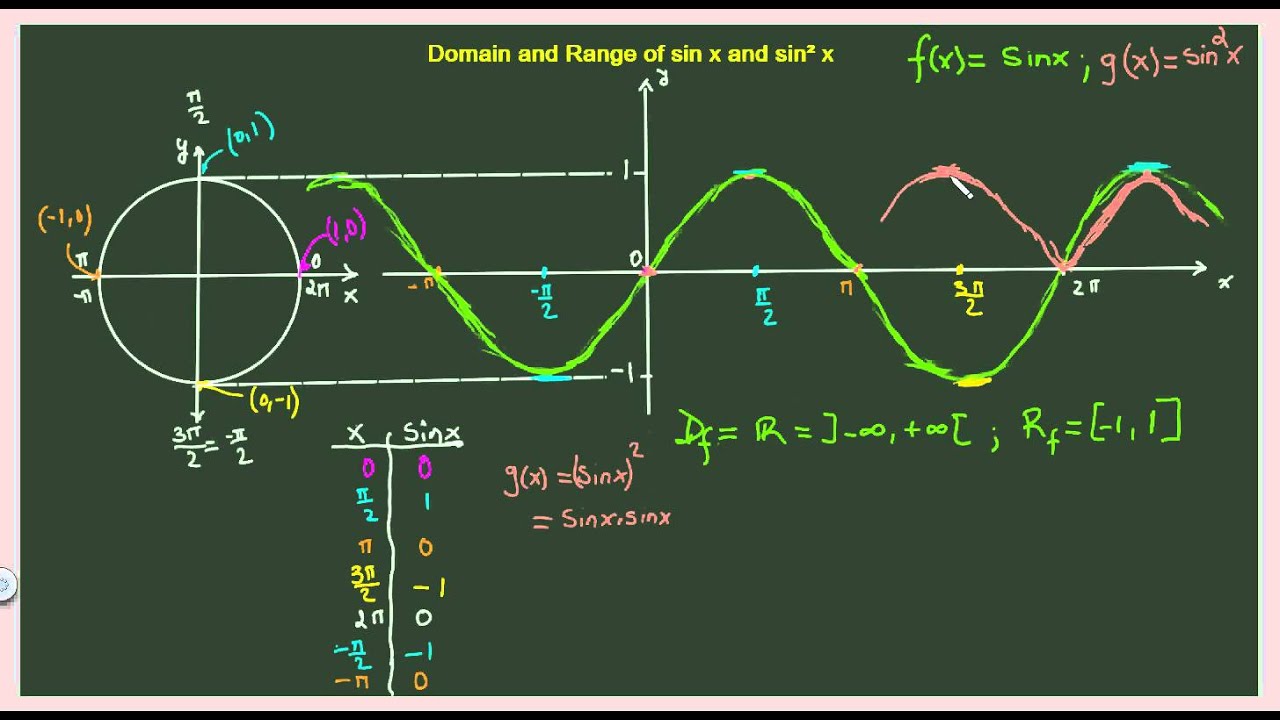



Trig Functions Domain And Range Of The Sin X And Sin X Function Youtube
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find the domain and range of the function `f(x)=1/(2sin3x)` Find the domain and range of $f(x)=\sin^{1}(\sqrt{x^2x1})$ Finding the domain $$x^2x1>=0 \text { it is always true }$$ $$1Find the domain and range of `f (x)=sqrt (cos (sin x))sin^1 ( (1x^2)/ (2x))` find the domain and range of `f (x)=sqrt (cos (sin x))sin^1 ( (1x^2)/ (2x))` Watch later Share Copy



Domain And Range Algebra And Trigonometry



Domain And Range Examples Domain And Range Of Functions
The domain of a function, D D, is most commonly defined as the set of values for which a function is defined For example, a function f (x) f ( x) that is defined for real values x x in R R has domain R R, and is sometimes said to be "a function over the reals" The set of values to which D D is sent by the function isThese include the graph, domain, range, asymptotes (if any), symmetry, x and y intercepts and maximum and minimum points Sine Function f(x) = sin (x) Graph; The function f has a domain of 0,5and a range of 0,3 Start by sketching a potential graph of f Suppose the function k is defined as k(x)=f(x−3) Determine the domain and range of k Domain Range math A movie theater seats 500 people



Domain And Range Of A Function




Domain And Range Free Math Help
When it comes to the domain, the denominator of the function has to be different from 0 so we look for those x who make the denominator zero and we take them away when it comes to the Range the sine fonction can take any small values whichHence, for the trigonometric functions f(x)= sin x and f(x)= cos x, the domain will consist of the entire set of real numbers, as they are defined for all the real numbers The range of f(x) = sin x and f(x)= cos x will lie from 1 to 1, including both 1 and 1, ie1 ≤ sin x ≤11 ≤ cos x ≤1;2 De nition = sin 1(x) means sin( ) = xwhen 1 x 1 and ˇ 2 ˇ 2 2 cos 1(x) Domain 1;1 Range 0;ˇ De nition = cos 1(x) means cos( ) = xwhen 1 x 1 and 0 ˇ 3 tan 1(x) Domain R Range ( ˇˇ 2;



Graph Domain And Range Of Arcsin X Function




Graph The Function In Radians And Describe The Domain And Range Of The Function F X Sin X 5 Study Com
Domain all real numbers Range 1 , 1 Period = 2pi x intercepts x = k pi , where k is an integer y intercepts y = 0 maximum points (pi/2 2 k pi , 1) , where k is an integerGiven, f(x) = sin1x tan1x sec1xClearly, the domain of f(x) is x = ± 1Thus, the range is {f(1), f( 1)}, ie π4, 3π4 Previous Year Papers Download Solved Question Papers Free for Offline Practice and view Solutions Online Test Series Take Zigya Full and Sectional Test Series Time it out for real assessment and get your results For x = 0 x = 0 So, f (x) = 0 Now, Plotting graph Here, Domain = All values of x = R Range = All values of y Since y will have value 0, 1 or –1



Domain And Range Examples Domain And Range Of Functions




Domain Range Of Trigonometric Functions Their Inverses Video Lesson Transcript Study Com
Domain Domain of the function f(x) will be the intersection of domains of sinx and cosx As the domain of sinx as well as cosx is (∞,∞), thus the domain of the funtion f(x) will the the intersection of the two domains which comes out to be (∞,∞) that is, that x can take any real value ranging from ∞ to ∞ Explanation This video might help enter link description here Answer link Rhys Domain −1 ≤ x ≤ 1 Range − π 2 ≤ y ≤ π 2The domain and range for any equation can be defined as If y = f (x), The possible attainable values of y is called Range The possible values of variable x with respect to the function is called Domain For the given question, we can write y = sin (x) ——— (1) Sin (x) always lies between
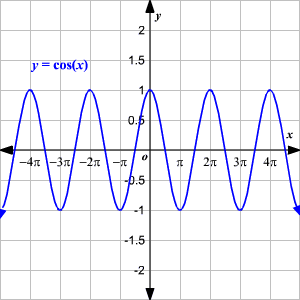



Trigonometric Functions




Find Domain And Range Of Sine Inverse 5x 1 Youtube
Cos x \displaystyle \cos x cosx is all the real numbers, therefore the domain of f ( x) = sin x cos x \displaystyle f (x)=\sin x\cos x f (x) = sinxcosx is all the real numbers, too Now for finding the range of f \displaystyle f f, one should know the formula which is given below The graph of the cotangent function looks like this The domain of the function y=cot (x)=cos (x)sin (x) is all real numbers except the values where sin (x) is equal to 0 , that is, the values πn for all integers n The range of the function is all real numbers Therefore, the range of f(x) is the union of the range of the two pieces, namely y > 1 (When x = 15, y = 1, so y = 1 is clearly in the range of f(x)) I ended up making a table of values in a spreadsheet to determine the range It seems that the fact that the function is fractional with an absolute value is throwing us off
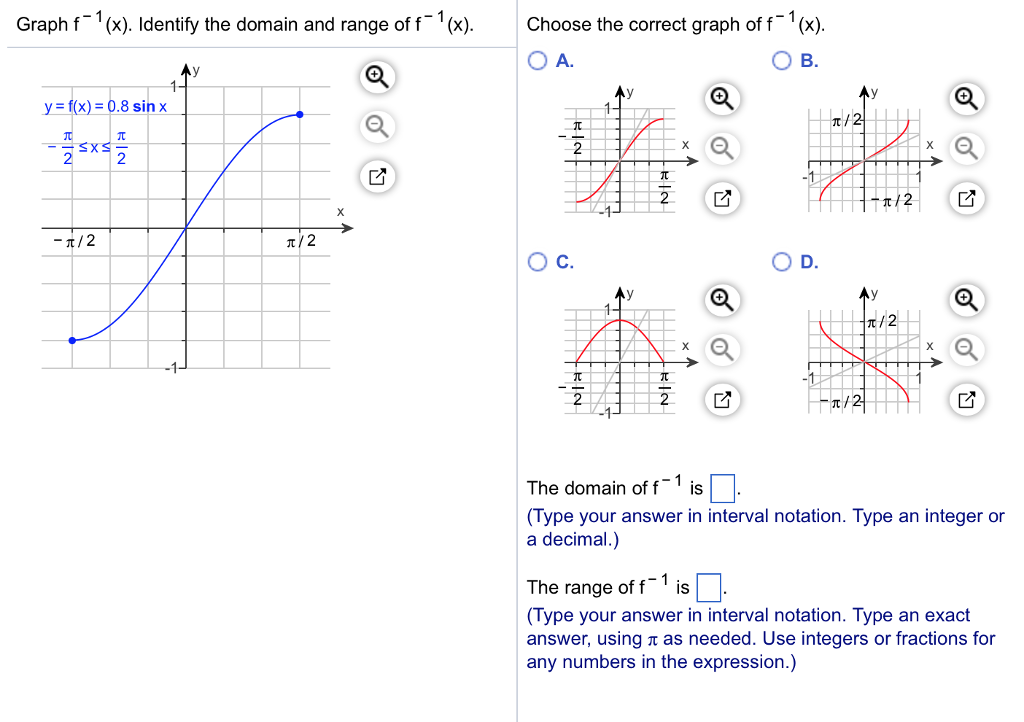



Graph F X Identify The Domain And Range Of F X Chegg Com




4 Ways To Find The Range Of A Function Wikihow
The Codomain is actually part of the definition of the function And The Range is the set of values that actually do come out Example we can define a function f (x)=2x with a domain and codomain of integers (because we say so) But by thinking about it we can see that the range (actual output values) is just the even integers




Given F X Sec X And G X Sin X What Is The Chegg Com




Find The Domain And Range Of The Inverse Of The Given Chegg Com




Find The Domain And Range Of The Function F X 2x Sin X Brainly Com



Determine Domain And Range From A Graph College Algebra




Domain And Range Of Trigonometric Functions



Jaxon Precal



How To Find The Domain And Range Of Sinx Cosx Quora



1



Properties Of The Six Trigonometric Functions



Graphs Of Trigonometric Functions The Graph Of The Sine Function F X Sin X Properties Of The Sine Function Parity And Periodicity Of The Sine Function Behavior Of The Sine Function



2
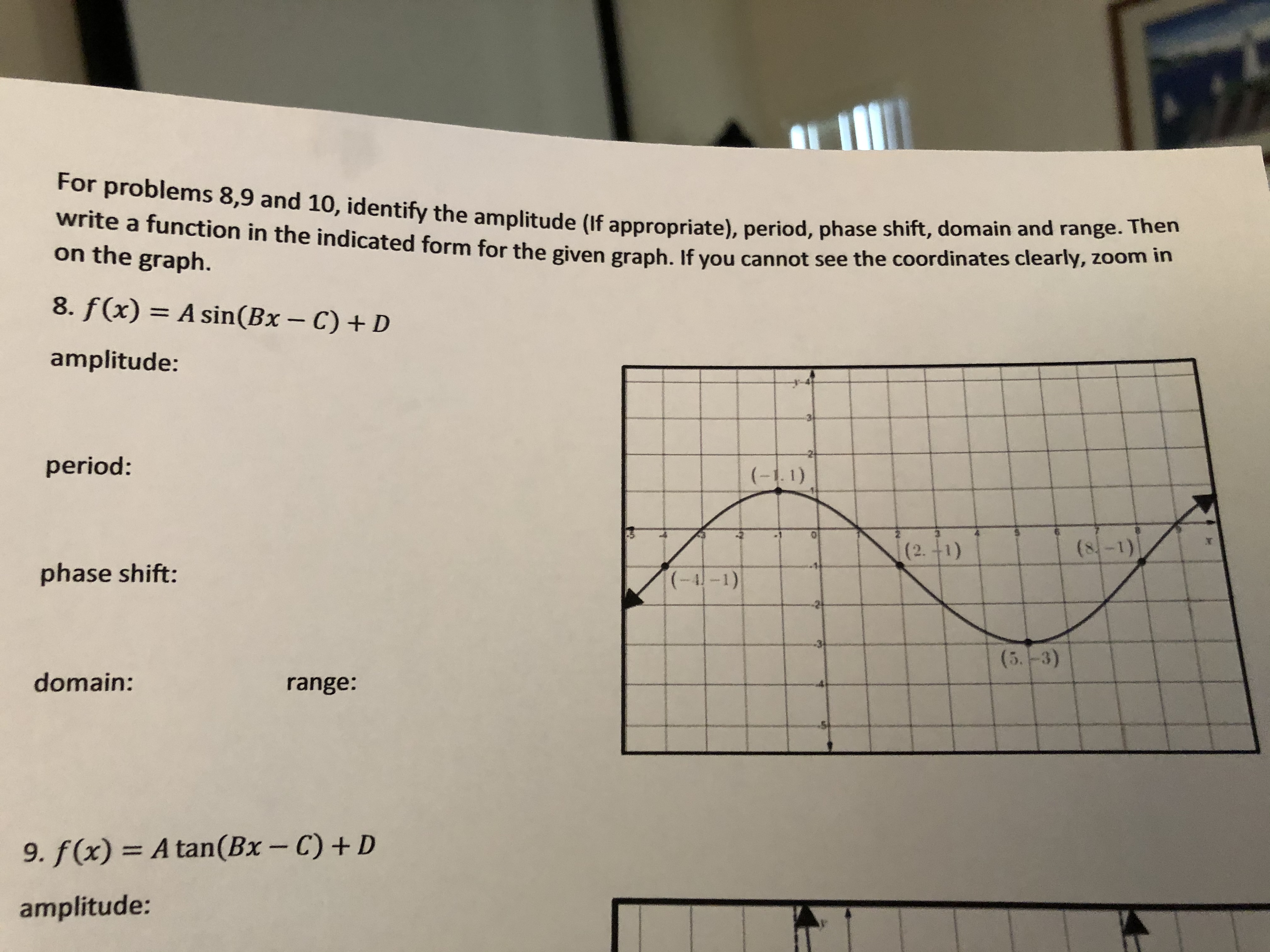



Answered 8 F X A Sin Bx C D 3d Bartleby



Domain And Range Of The Sin X And Sin X Function Video Dailymotion




Exercise I 1 Find The Domain Range Of The Following Math



Domain And Range And Composition Of Functions




6 6 Trig Inverses And Their Graphs Ppt Video Online Download



How To Find The Domain And Range Of Sin X Quora




Domain And Range Of Inverse Trigonometric Functions



Copy Of Graphing Trigonometric Functions Ii Teacher Guide




Domain And Range Of Trigonometric Functions And Their Graphs W3spoint




Inverses Of Trigonometric Functions Ck 12 Foundation




12x1 T05 02 Inverse Trig Functions 10
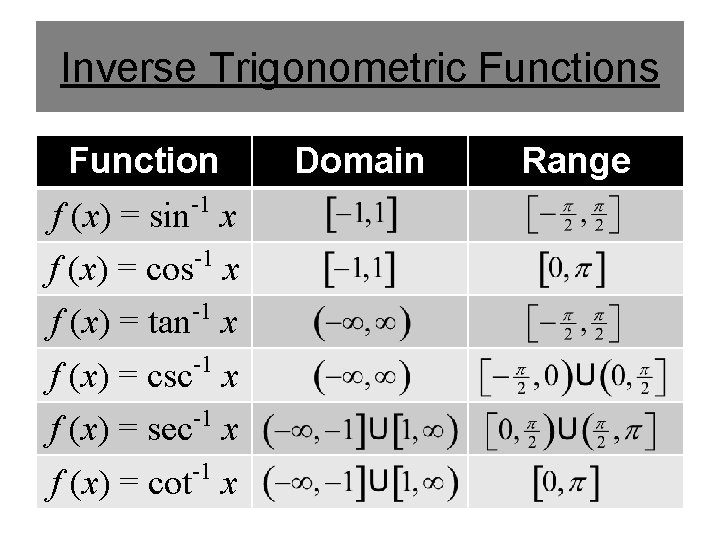



Inverse Functions Inverse Relations The Inverse Of A




Inverses Of The Trigonometric Functions
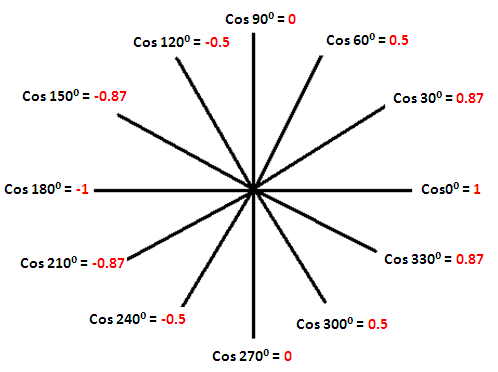



Domain And Range Of Trigonometric Functions
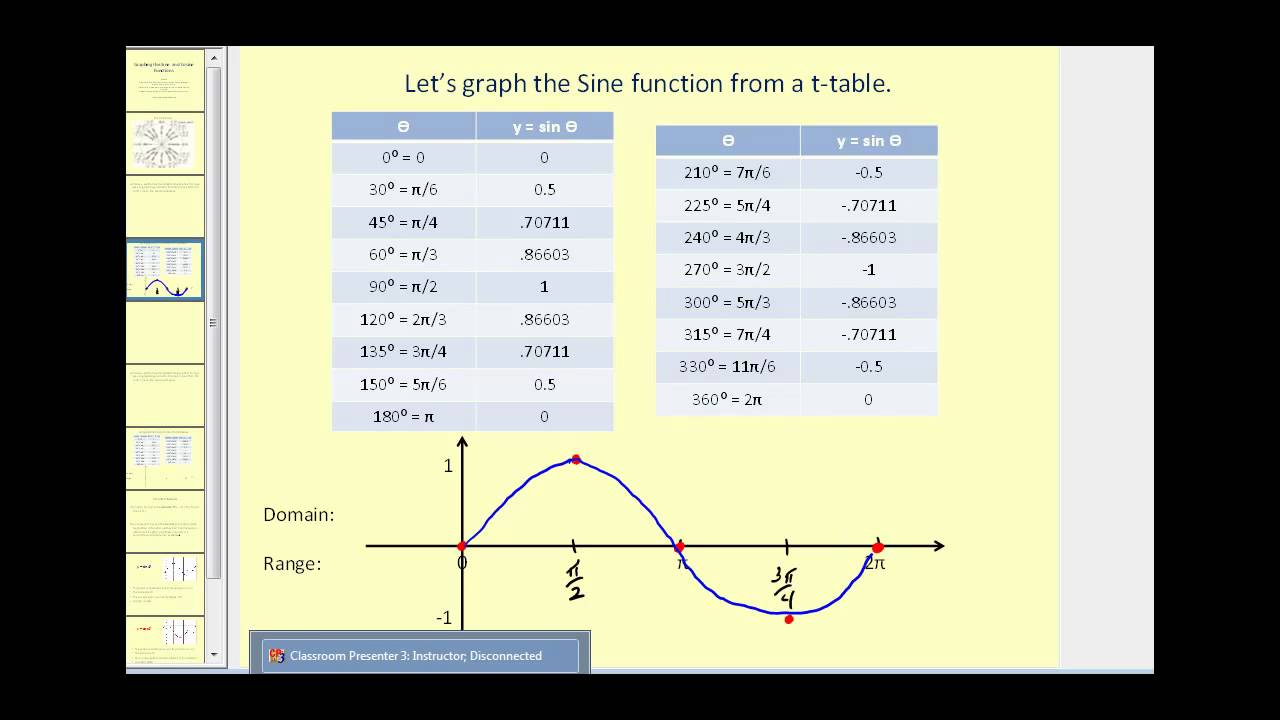



Sine Cosine Tangent Graphs Video Lessons Examples And Solutions




How To Find A Domain And Range Of A Function Arxiusarquitectura




F X Sqareroot Of Sin X Cos X Find Domain And Range Mathematics Topperlearning Com Yskun1qq




Domain Range Of Trigonometric Functions Their Inverses Video Lesson Transcript Study Com




Graph Of Y Sin X Video Trigonometry Khan Academy



Q Tbn And9gcqwnhucnqrdknrxnm Mul21cigtavfvwpgvxpkzf1c Bfbbbkij Usqp Cau




Is The Function F X Sec X And G X Sin X What Is The Composed Function F G X Sec Sin X And Brainly Com




Finding The Domain And Range Of A Function Graphically Expii



Graph Of Inverse Sine Function




Consider The Real Valued Function Satisfying Math 2f Sin X F Cos X X Math The Domain Of Math F Math Is Math 1 1 Math What S The Range Of Math F Math Quora




How To Find Domain And Range Of Sine Cosine And Tangent Youtube



Graphing Arcsin X Functions




Find The Range Of Sin Sinx
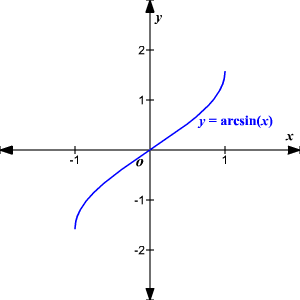



Inverse Trigonometric Functions




Domain And Range Of Trigonometric Functions Videos Solved Examples




Graphs Of Trig Functions She Loves Math




Domain And Range Of Trigonometric Functions Videos Solved Examples




Find The Domain And Range Of F X Sqrt Cos Sin X Sin 1 1 X 2 2x Youtube




2 A Graph The Function F X Sin X Is It Chegg Com




Find Domain And Range F X 1 2 Sin 3x Maths Relations And Functions Meritnation Com




Domain And Range Of Functions




Y 3 Sin X Domain And Range



Graph Domain And Range Of Arcsin X Function



Domain Of A Function Wikipedia




Find The Domain And Range Of The Function F X Sin X



Www Askiitians Com Forums Differential Calculus 25 Functions Htm



Visualizing Domain And Range



1




Domain And Range Calculator Wolfram Alpha



Www Wcde Org Cms Lib Tn Centricity Domain 295 Ccf Pdf



Functions A Function Is A Relationship Between Two Sets The Domain Input And The Range Output Domainrange Input Output This Ppt Download



Domain Range And Graphs Of Trigonometric Functions
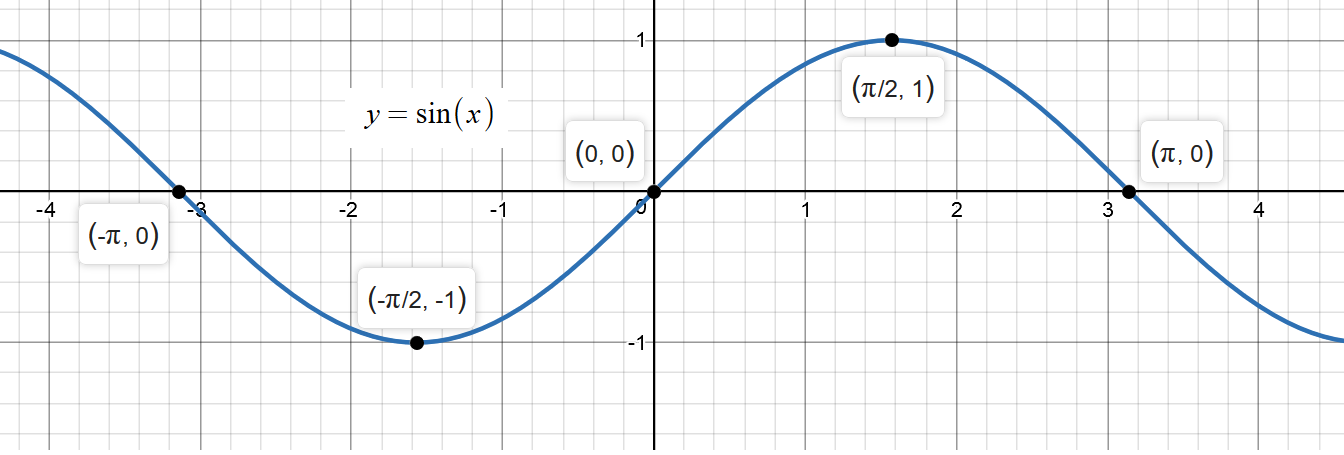



How Do You Graph Y Sin3x Socratic



Graphs Of The Sine And Cosine Function Precalculus Ii




How To Find The Domain And Range Of Sinx Cosx Quora
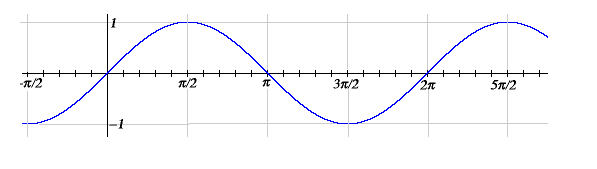



Domain Range And Graphs Of Trigonometric Functions




Find The Domain And Range Of F X 1 Sin X Find Chegg Com
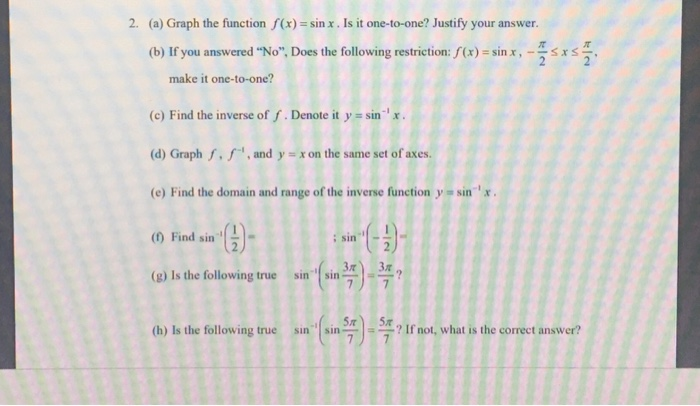



2 A Graph The Function F X Sin X Is It Chegg Com




Inverse Trigonometric Functions




Domain And Range Free Math Help



What Is The Domain And Range Of Log Sin X Quora




Domain And Range Of Trigonometric Functions Videos Solved Examples



Find The Range Of The Function F X Log 5 2 Sin X Cos X 3 Sarthaks Econnect Largest Online Education Community



Domain Range And Graphs Of Trigonometric Functions




Find The Domain And Range Of The Function F X Sin 1 X 2 2



Links Forward Inverse Trigonometric Functions




6 6 Trig Inverses And Their Graphs Ppt Video Online Download




Graphs Of Sine Function Mathtestpreparation Com



What Is The Domain And Range Of Log Sin X Quora



Precalculus Trigonometric Functions Graphs Sparknotes




The Sine Cosine And Tangent Functions



0 件のコメント:
コメントを投稿